题目内容
3.已知点A(1,5),B(3,1),点M在x轴上,当AM+BM最小时,点M的坐标为($\frac{8}{3}$,0).分析 根据两点之间线段最短,先找到点B关于x轴的对称点B′,再连接AB′,则AB′与x轴的交点即为所求点M.
解答  解:点B关于x轴对称的点的坐标是B′(3,-1).
解:点B关于x轴对称的点的坐标是B′(3,-1).
连AB′,则AB′与x轴的交点M即为所求.
设AB′所在直线的解析式为y=kx+b,
则$\left\{\begin{array}{l}{k+b=5}\\{3k+b=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-3}\\{b=8}\end{array}\right.$.
所以直线AB′的解析式为y=-3x+8,
当y=0时,x=$\frac{8}{3}$.
故所求的点为M$(\frac{8}{3},0)$.
故答案为:($\frac{8}{3}$,0).
点评 本题考查了轴对称--最短路线问题、坐标与图形性质,待定系数法求一次函数解析式,准确求出点M的位置是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
11.到三角形三边的距离相等的点P应是三角形的三条( )的交点.
| A. | 角平分线 | B. | 高 | C. | 中线 | D. | 垂直平分线 |
8. 如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,∠AEC等于( )
如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,∠AEC等于( )
 如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,∠AEC等于( )
如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,∠AEC等于( )| A. | 56° | B. | 66° | C. | 76° | D. | 无法确定 |
12. 如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )
如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )
 如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )
如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )| A. | 100° | B. | 110° | C. | 125° | D. | 135° |
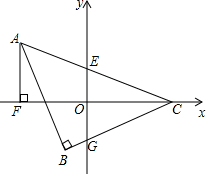 如图,将△ABC放置在平面直角坐标系中,点C在x轴上,∠ABC=90°,∠ACB=45°,AB=BC,x轴平分∠ACB,AC交y轴于点E,BC交y轴于点G,AB交x轴于点H.
如图,将△ABC放置在平面直角坐标系中,点C在x轴上,∠ABC=90°,∠ACB=45°,AB=BC,x轴平分∠ACB,AC交y轴于点E,BC交y轴于点G,AB交x轴于点H.