题目内容
 如图,菱形ABCD中,对角线AC与BD相交于点O,点E,F,M,N分别为四边的中点,试说明:E,F,M,N四点在同一个圆上.
如图,菱形ABCD中,对角线AC与BD相交于点O,点E,F,M,N分别为四边的中点,试说明:E,F,M,N四点在同一个圆上.考点:四点共圆
专题:证明题
分析:要证E,F,M,N四点在同一个圆上,只需证明OE=OF=ON=OM,只需运用直角三角形斜边上的中线等于斜边的一半就可解决问题.
解答:证明:∵四边形ABCD是菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴∠AOB=∠BOC=∠COD=∠DOA=90°.
∵点E、F、N、M分别为四边的中点,
∴OE=
AB,OF=
BC,ON=
CD,OM=
AD,
∴OE=OF=ON=OM,
∴E、F、M、N四点在以点O为圆心,OE为半径的圆上,
∴E、F、M、N四点在同一个圆上.
∴AC⊥BD,AB=BC=CD=DA,
∴∠AOB=∠BOC=∠COD=∠DOA=90°.
∵点E、F、N、M分别为四边的中点,
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OE=OF=ON=OM,
∴E、F、M、N四点在以点O为圆心,OE为半径的圆上,
∴E、F、M、N四点在同一个圆上.
点评:本题主要考查了菱形的性质、直角三角形斜边上的中线等于斜边的一半、四点共圆的判定等知识,解决本题的关键是找到一个点,使得该点到E、F、M、N四点的距离都相等.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
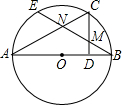 如图,AB为⊙O的直径,C为半圆上一点,且CD⊥AB于点B,E为
如图,AB为⊙O的直径,C为半圆上一点,且CD⊥AB于点B,E为
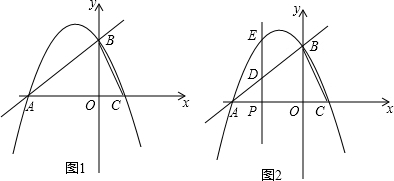
 如图,直角坐标系中,Rt△ABC的边在x轴上,∠CAB=90°,tan∠ACB=
如图,直角坐标系中,Rt△ABC的边在x轴上,∠CAB=90°,tan∠ACB=