题目内容
 如图,在△ABC中,∠A=30°,∠B=45°,AC=2
如图,在△ABC中,∠A=30°,∠B=45°,AC=2| 3 |
考点:解直角三角形
专题:
分析:如图,过点C作CD⊥AB于点D.通过解直角△ACD求得CD、AD的长度,通过解直角△BCD求得BD的长度;则易求AB=AD+BD;然后由三角形面积公式进行解答.
解答: 解:如图,过点C作CD⊥AB于点D.
解:如图,过点C作CD⊥AB于点D.
∵在直角△ACD中,∠A=30°,AC=2
,
∴AD=AC•cos30°=2
×
=3,CD=
AC=
.
∵在直角△BCD中,∠B=45°,CD=
,
∴BD=CD=
,
∴AB=AD+BD=3+
∴S△ABC=
AB•CD=
×(3+
)×
=
.
故答案是:
.
 解:如图,过点C作CD⊥AB于点D.
解:如图,过点C作CD⊥AB于点D.∵在直角△ACD中,∠A=30°,AC=2
| 3 |
∴AD=AC•cos30°=2
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∵在直角△BCD中,∠B=45°,CD=
| 3 |
∴BD=CD=
| 3 |
∴AB=AD+BD=3+
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
3+3
| ||
| 2 |
故答案是:
3+3
| ||
| 2 |
点评:本题考查了解直角三角形.对于此类题目,不是直角三角形,要利用三角函数必须构筑直角三角形,知道三个元素(至少有一个是边),就能求出其余的边和角.进而求面积,在转化时,尽量不要破坏所给条件.

练习册系列答案
相关题目
2014年2月我国出口1141亿美元,进口1370.8亿美元,贸易逆差229.8亿美元,用科学记数法表示-229.8亿美元(保留3个有效数字)( )
| A、-2.29×1010 |
| B、-2.30×1010 |
| C、-2.3×109 |
| D、-2.30×109 |
 如图,已知△ABC.
如图,已知△ABC. 某校一周中五天的用水量如图,则该校这五天的平均用水量是
某校一周中五天的用水量如图,则该校这五天的平均用水量是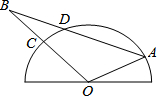 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,∠B的度数为
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,∠B的度数为