题目内容
11.一直角三角形的斜边比一直角边大4,另一直角边长为8,则斜边长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 设一条直角边为a,则斜边为a+4,再根据勾股定理求出a的值即可.
解答 解:设一条直角边为a,则斜边为a+4,
∵另一直角边长为8,
∴(a+4)2=a2+82,解得a=6,
∴a+4=10.
故选C.
点评 本题考查的是勾股定理,根据题意设出直角三角形的斜边及直角边的长是解答此题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
6.甲、乙两农户是某农业合作社社员,他们今年种植了新型豌豆和土豆,他们生产的农产品由合作社分别以x万元/吨,y万元/吨的价格收购,他们今年种植面积、亩产量与卖出农产品的总收入如下表:
(1)求x、y的值;
(2)为了以进一步调动农户的种植热情,合作社计划明年炸收购价不变的情况下对种植这两种农产品给予补贴,补贴标准如下:种植豌豆每亩补贴0.06万元,种植土豆每亩补贴0.05万元,甲种植户计划租30亩地用来种植豌豆和土豆,合作社要求豌豆的种植面积低于土豆的种植面积(两种产品的种植面积均为整数亩),每亩产量均保持不变),为了使甲总收入不低于19.62万元,则他有几种种植方案,并指出哪种种植方案收入最高?
| 种植户 | 豌豆 | 土豆 | 卖出两种农产品总收入(万元) | ||
| 种植面积(亩) | 每亩产量(吨) | 种植面积(亩) | 每亩产量(吨) | ||
| 甲 | 4 | 1 | 4 | 3 | 4.8 |
| 乙 | 8 | 1 | 2 | 2.5 | 5.8 |
(2)为了以进一步调动农户的种植热情,合作社计划明年炸收购价不变的情况下对种植这两种农产品给予补贴,补贴标准如下:种植豌豆每亩补贴0.06万元,种植土豆每亩补贴0.05万元,甲种植户计划租30亩地用来种植豌豆和土豆,合作社要求豌豆的种植面积低于土豆的种植面积(两种产品的种植面积均为整数亩),每亩产量均保持不变),为了使甲总收入不低于19.62万元,则他有几种种植方案,并指出哪种种植方案收入最高?
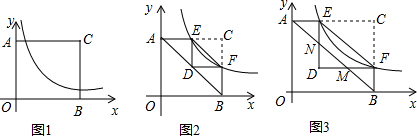
1. 已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线与边BC交于点D、与对角线OB交于点中点E,若△OBD的面积为10,则k的值是( )
已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线与边BC交于点D、与对角线OB交于点中点E,若△OBD的面积为10,则k的值是( )
 已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线与边BC交于点D、与对角线OB交于点中点E,若△OBD的面积为10,则k的值是( )
已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线与边BC交于点D、与对角线OB交于点中点E,若△OBD的面积为10,则k的值是( )| A. | 10 | B. | 5 | C. | $\frac{10}{3}$ | D. | $\frac{20}{3}$ |
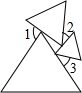 三个等边三角形的位置如图所示,若∠3=40°,则∠1+∠2=140°.
三个等边三角形的位置如图所示,若∠3=40°,则∠1+∠2=140°. 如图,E、F是?ABCD对角线AC上的两点,AF=CE.求证:BE=DF.
如图,E、F是?ABCD对角线AC上的两点,AF=CE.求证:BE=DF.