题目内容
19.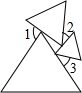 三个等边三角形的位置如图所示,若∠3=40°,则∠1+∠2=140°.
三个等边三角形的位置如图所示,若∠3=40°,则∠1+∠2=140°.
分析 先根据图中是三个等边三角形可知三角形各内角等于60°,用∠1,∠2,∠3表示出△ABC各角的度数,再根据三角形内角和定理即可得出结论.
解答 解:∵图中是三个等边三角形,∠3=40°,
∴∠ABC=180°-60°-40°=80°,∠ACB=180°-60°-∠2=120°-∠2,
∠BAC=180°-60°-∠1=120°-∠1,
∵∠ABC+∠ACB+∠BAC=180°,
∴80°+(120°-∠2)+(120°-∠1)=180°,
∴∠1+∠2=140°.
故答案为:140
点评 本题考查的是等边三角形的性质,熟知等边三角形各内角均等于60°是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.对于反比例函数y=-$\frac{2}{x}$,下列说法正确的是( )
| A. | 图象经过(1,2) | B. | 当x>0时,y随着x的增大而减小 | ||
| C. | 图象位于一、三象限 | D. | 该函数图象是中心对称图形 |
11.一直角三角形的斜边比一直角边大4,另一直角边长为8,则斜边长为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
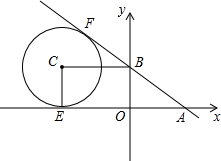 如图,在平面直角坐标系xOy中,直线y=$-\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B.
如图,在平面直角坐标系xOy中,直线y=$-\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B.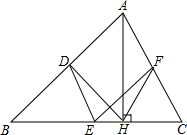 如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.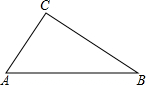 如图所示,在△ABC中,∠ACB=90°
如图所示,在△ABC中,∠ACB=90°