题目内容
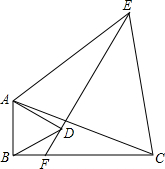 在△ABC中,∠ABC=90°,以直角边AB向内作等边△ABD,以斜边AC向外作等边△ACE,连接ED,并延长ED与BC相交于点F,求∠EFC的度数.
在△ABC中,∠ABC=90°,以直角边AB向内作等边△ABD,以斜边AC向外作等边△ACE,连接ED,并延长ED与BC相交于点F,求∠EFC的度数.考点:全等三角形的判定与性质
专题:
分析:如图,证明△ABC≌△ADE,得到∠ADE=∠ABC=90°;进而证明∠ABF+∠ADF=180°,得到A、B、F、D四点共圆,问题即可解决.
解答: 解:如图,∵△ABD和△ACE均为等边三角形,
解:如图,∵△ABD和△ACE均为等边三角形,
∴AB=AD; AE=AC;∠BAD=∠CAE=60°;
∴∠BAC=∠BAD+∠DAC=∠BAD+∠CAE=∠DAE;
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS),
∴∠ADE=∠ABC=90°,
∴∠ABF+∠ADF=180°,
A、B、F、D四点共圆,
∴∠EFC=∠BAD=60°.
 解:如图,∵△ABD和△ACE均为等边三角形,
解:如图,∵△ABD和△ACE均为等边三角形,∴AB=AD; AE=AC;∠BAD=∠CAE=60°;
∴∠BAC=∠BAD+∠DAC=∠BAD+∠CAE=∠DAE;
在△ABC和△ADE中,
|
∴△ABC≌△ADE(SAS),
∴∠ADE=∠ABC=90°,
∴∠ABF+∠ADF=180°,
A、B、F、D四点共圆,
∴∠EFC=∠BAD=60°.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是深刻分析,大胆猜测推理,科学求解论证.

练习册系列答案
相关题目
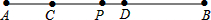 如图所示,C,D是线段AB上的两点,AC:CD:DB=2:3:4,P是线段AB的中点,若PD=2厘米,求:
如图所示,C,D是线段AB上的两点,AC:CD:DB=2:3:4,P是线段AB的中点,若PD=2厘米,求: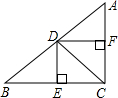 如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB,过点D分别作DE⊥BC,DF⊥AC,垂足分别为E,F.
如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB,过点D分别作DE⊥BC,DF⊥AC,垂足分别为E,F.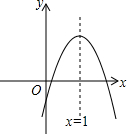 已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c>0;④(a+c)2<b2,正确的是
已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c>0;④(a+c)2<b2,正确的是