题目内容
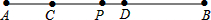 如图所示,C,D是线段AB上的两点,AC:CD:DB=2:3:4,P是线段AB的中点,若PD=2厘米,求:
如图所示,C,D是线段AB上的两点,AC:CD:DB=2:3:4,P是线段AB的中点,若PD=2厘米,求:(1)PD:PC的值;
(2)线段CD的长;
(3)线段AB的长.
考点:两点间的距离
专题:
分析:(1)设AC=2x,则CD=3x,DB=4x,则AB=AC+CD+BD=9x,根据线段中点的定义得AP=BP=
AB=
x,于是可计算出PD=BP-BD=
x,PC=AP-AC=
x,然后计算PD:PC的值;
(2)先由PD=2cm得到
x=2,解得x=4,然后利用CD=3x进行计算;
(3)利用AB=9x进行计算.
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
(2)先由PD=2cm得到
| 1 |
| 2 |
(3)利用AB=9x进行计算.
解答:解:(1)设AC=2x,则CD=3x,DB=4x,
∴AB=AC+CD+BD=9x,
∵P是线段AB的中点,
∴AP=BP=
AB=
x,
∴PD=BP-BD=
x-4x=
x,PC=AP-AC=
x-2x=
x,
∴PD:PC=
x:
x=1:5;
(2)∵PD=2cm,
∴
x=2,解得x=4,
∴CD=3x=12cm;
(3)AB=9x=36cm.
∴AB=AC+CD+BD=9x,
∵P是线段AB的中点,
∴AP=BP=
| 1 |
| 2 |
| 9 |
| 2 |
∴PD=BP-BD=
| 9 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 5 |
| 2 |
∴PD:PC=
| 1 |
| 2 |
| 5 |
| 2 |
(2)∵PD=2cm,
∴
| 1 |
| 2 |
∴CD=3x=12cm;
(3)AB=9x=36cm.
点评:本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.注意强调最后的两个字“长度”,也就是说,距离是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.常用代数法计算距离.

练习册系列答案
相关题目
下列命题中是假命题的是( )
| A、平行四边形的对边相等 |
| B、菱形的四条边相等 |
| C、矩形的对边平行且相等 |
| D、平行四边形的对角线相等 |
 如图,在△OAB中,∠AOB=25°,将△OAB绕点顶O顺时针旋转60°得到△COD,观察图形并回答问题:
如图,在△OAB中,∠AOB=25°,将△OAB绕点顶O顺时针旋转60°得到△COD,观察图形并回答问题: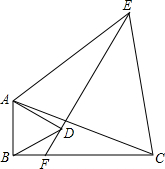 在△ABC中,∠ABC=90°,以直角边AB向内作等边△ABD,以斜边AC向外作等边△ACE,连接ED,并延长ED与BC相交于点F,求∠EFC的度数.
在△ABC中,∠ABC=90°,以直角边AB向内作等边△ABD,以斜边AC向外作等边△ACE,连接ED,并延长ED与BC相交于点F,求∠EFC的度数.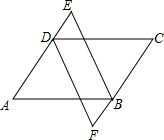 如图所示,在四边形ABCD中,已知AB=CD,AD=BC,DE=BF,且点E、F分别在AD、CB的延长线上.求证:BE=DF.
如图所示,在四边形ABCD中,已知AB=CD,AD=BC,DE=BF,且点E、F分别在AD、CB的延长线上.求证:BE=DF. 如图,数轴上的A,B,C三点所表示的数分别是a,b,c,其中AB=BC,若|a|>|b|>|c|,则该数轴的原点O的位置应该在
如图,数轴上的A,B,C三点所表示的数分别是a,b,c,其中AB=BC,若|a|>|b|>|c|,则该数轴的原点O的位置应该在