题目内容
在Rt△ABC中,AB=AC,点D,E是线段AC上两动点,且AD=EC,AM⊥BD,垂足为M,AM的延长线交BC于点N,直线BD与直线NE相交于点F.试判断△DEF的形状,并加以证明.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:如图,作辅助线,首先证明△BAD≌△ACP,得到AD=CP,∠ADB=∠P,进而得到CE=CP;证明△CPN≌△CEN 得到∠P=∠CEN,问题即可解决.
解答: 解:△DEF是等腰三角形.
解:△DEF是等腰三角形.
证明:如图,过点C作CP⊥AC,交AN延长线于点P
在Rt△ABC中,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,∠PCN=∠ACB=45°,∠BAD=∠ACP
∵AM⊥BD,
∴∠ABD+∠BAM=∠BAM+∠CAP=90°,
∴∠ABD=∠CAP,
在△BAD与△ACP 中,
,
∴△BAD≌△ACP (ASA),
∴AD=CP,∠ADB=∠P;
∵AD=CE,
∴CE=CP;
在△CPN与△CEN中,
,
∴△CPN≌△CEN (SAS),
∴∠P=∠CEN,∠CEN=∠ADB,
∵∠ADB=∠CEN,
∴∠FDE=∠FED,
∴△DEF是等腰三角形.
 解:△DEF是等腰三角形.
解:△DEF是等腰三角形.证明:如图,过点C作CP⊥AC,交AN延长线于点P
在Rt△ABC中,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,∠PCN=∠ACB=45°,∠BAD=∠ACP
∵AM⊥BD,
∴∠ABD+∠BAM=∠BAM+∠CAP=90°,
∴∠ABD=∠CAP,
在△BAD与△ACP 中,
|
∴△BAD≌△ACP (ASA),
∴AD=CP,∠ADB=∠P;
∵AD=CE,
∴CE=CP;
在△CPN与△CEN中,
|
∴△CPN≌△CEN (SAS),
∴∠P=∠CEN,∠CEN=∠ADB,
∵∠ADB=∠CEN,
∴∠FDE=∠FED,
∴△DEF是等腰三角形.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是作辅助线,构造全等三角形,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
如果某家用电冰箱冷藏室的温度是5℃,冷冻室的温度比冷藏室的温度低20℃,则冷冻室的温度为( )
| A、-25℃ | B、-20℃ |
| C、-15℃ | D、-10℃ |
由四舍五入得到的近似数是3.20×104,这个近似数精确到( )
| A、百分位 | B、万位 | C、千位 | D、百位 |
 如图,在△OAB中,∠AOB=25°,将△OAB绕点顶O顺时针旋转60°得到△COD,观察图形并回答问题:
如图,在△OAB中,∠AOB=25°,将△OAB绕点顶O顺时针旋转60°得到△COD,观察图形并回答问题: 在一个棱长为3cm的立方体纸箱的A点有一只蜘蛛看见一只蚂蚁从纸箱B点沿BC往C点爬行,如果蚂蚁的爬行速度为1cm/s,蜘蛛的爬行速度为2cm/s,请你分析一下,蜘蛛沿纸箱表面爬去捉住蚂蚁的最短时间是多少秒?
在一个棱长为3cm的立方体纸箱的A点有一只蜘蛛看见一只蚂蚁从纸箱B点沿BC往C点爬行,如果蚂蚁的爬行速度为1cm/s,蜘蛛的爬行速度为2cm/s,请你分析一下,蜘蛛沿纸箱表面爬去捉住蚂蚁的最短时间是多少秒?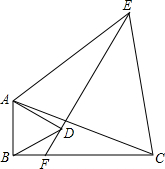 在△ABC中,∠ABC=90°,以直角边AB向内作等边△ABD,以斜边AC向外作等边△ACE,连接ED,并延长ED与BC相交于点F,求∠EFC的度数.
在△ABC中,∠ABC=90°,以直角边AB向内作等边△ABD,以斜边AC向外作等边△ACE,连接ED,并延长ED与BC相交于点F,求∠EFC的度数.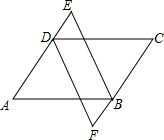 如图所示,在四边形ABCD中,已知AB=CD,AD=BC,DE=BF,且点E、F分别在AD、CB的延长线上.求证:BE=DF.
如图所示,在四边形ABCD中,已知AB=CD,AD=BC,DE=BF,且点E、F分别在AD、CB的延长线上.求证:BE=DF.