题目内容
已知:在△ABC中,∠C=90°,三边长为a,b,c,△ABC的内切圆半径为r,求证:
(1)r=
(a+b-c);
(2)r=
.
(1)r=
| 1 |
| 2 |
(2)r=
| ab |
| a+b+c |
考点:三角形的内切圆与内心
专题:证明题
分析:(1)作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,根据切线的性质得OD=OE=OF=r,再证明四边形CEOF为正方形,所以CE=CF=r,然后根据切线长定理得AE=AD=b-r,BF=BD=a-r,则b-r+a-r=c,所以r=
(a+b-c);
(2)连结OA、OB、OC,如图,根据三角形面积公式和S△AOB+S△BOC+S△AOC=S△AOB得到
•r•c+
•r•a+
•r•b=
•a•b,然后变形即可得到结论.
| 1 |
| 2 |
(2)连结OA、OB、OC,如图,根据三角形面积公式和S△AOB+S△BOC+S△AOC=S△AOB得到
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:(1) 作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,
作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,
∵⊙O为△ABC的内切圆,
∴OD=OE=OF=r,
∵∠ACB=90°,
∴四边形CEOF为正方形,
∴CE=CF=r,
∴AE=AD=b-r,BF=BD=a-r,
∴b-r+a-r=c,
∴r=
(a+b-c);
(2)连结OA、OB、OC,如图,
∵S△AOB+S△BOC+S△AOC=S△AOB,
∴
•r•c+
•r•a+
•r•b=
•a•b,
∴r=
.
 作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,
作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,∵⊙O为△ABC的内切圆,
∴OD=OE=OF=r,
∵∠ACB=90°,
∴四边形CEOF为正方形,
∴CE=CF=r,
∴AE=AD=b-r,BF=BD=a-r,
∴b-r+a-r=c,
∴r=
| 1 |
| 2 |
(2)连结OA、OB、OC,如图,
∵S△AOB+S△BOC+S△AOC=S△AOB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| ab |
| a+b+c |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.熟练运用切线的性质.

练习册系列答案
相关题目
由四舍五入得到的近似数是3.20×104,这个近似数精确到( )
| A、百分位 | B、万位 | C、千位 | D、百位 |
 如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合.
如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合. 如图,在△OAB中,∠AOB=25°,将△OAB绕点顶O顺时针旋转60°得到△COD,观察图形并回答问题:
如图,在△OAB中,∠AOB=25°,将△OAB绕点顶O顺时针旋转60°得到△COD,观察图形并回答问题: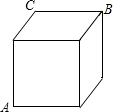 在一个棱长为3cm的立方体纸箱的A点有一只蜘蛛看见一只蚂蚁从纸箱B点沿BC往C点爬行,如果蚂蚁的爬行速度为1cm/s,蜘蛛的爬行速度为2cm/s,请你分析一下,蜘蛛沿纸箱表面爬去捉住蚂蚁的最短时间是多少秒?
在一个棱长为3cm的立方体纸箱的A点有一只蜘蛛看见一只蚂蚁从纸箱B点沿BC往C点爬行,如果蚂蚁的爬行速度为1cm/s,蜘蛛的爬行速度为2cm/s,请你分析一下,蜘蛛沿纸箱表面爬去捉住蚂蚁的最短时间是多少秒?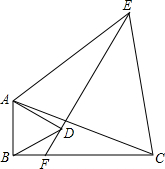 在△ABC中,∠ABC=90°,以直角边AB向内作等边△ABD,以斜边AC向外作等边△ACE,连接ED,并延长ED与BC相交于点F,求∠EFC的度数.
在△ABC中,∠ABC=90°,以直角边AB向内作等边△ABD,以斜边AC向外作等边△ACE,连接ED,并延长ED与BC相交于点F,求∠EFC的度数.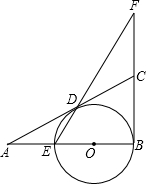 如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB长为半径的圆与AB交于点E,与AC相切于点D,直线ED交BC的延长线于点F.
如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB长为半径的圆与AB交于点E,与AC相切于点D,直线ED交BC的延长线于点F.