题目内容
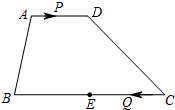 在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点,点P以每秒1个单位长度的速度从点A出发沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时点Q也随之停止运动.探究:在运动过程中,图中是否出现平行四边形?若能请写出平行四边形名称,并求出运动时间t;如不能,则说明理由.
在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点,点P以每秒1个单位长度的速度从点A出发沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时点Q也随之停止运动.探究:在运动过程中,图中是否出现平行四边形?若能请写出平行四边形名称,并求出运动时间t;如不能,则说明理由.考点:梯形,平行四边形的判定
专题:动点型,探究型,分类讨论
分析:分别从当PD=CQ时,四边形CDPQ是平行四边形,当Q运动到E和B之间,且PD=EQ时,四边形PDEQ是平行四边形,当Q运动到E和C之间,且PD=EQ时,四边形PDQE是平行四边形,当AP=BQ是,四边形ABQP是平行四边形去分析求解即可求得答案.
解答: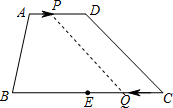 解:能出现平行四边形.
解:能出现平行四边形.
根据题意得:AP=t,CQ=3t,
则PD=AD-AP=6-t,BQ=BC-CQ=16-3t,
∵E是BC的中点,
∴CE=8,
∵AD∥BC,
∴①当PD=CQ时,四边形CDPQ是平行四边形,
即6-t=3t,
解得:t=1.5;
∴当t=1.5时,四边形CDPQ是平行四边形;
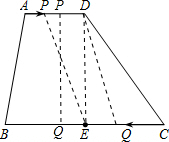 ②当Q运动到E和B之间,且PD=EQ时,四边形PDEQ是平行四边形,
②当Q运动到E和B之间,且PD=EQ时,四边形PDEQ是平行四边形,
即3t-8=6-t,
解得:t=3.5,
∴当t=3.5时,四边形PDEQ是平行四边形;
③当Q运动到E和C之间,且PD=EQ时,四边形PDQE是平行四边形,
即8-3t=6-t,
解得:t=1,
∴当t=1时,四边形PDQE是平行四边形;
④当AP=BQ是,四边形ABQP是平行四边形,
即t=16-3t,
解得:t=4,
∴当t=4时,四边形ABQP是平行四边形.
 解:能出现平行四边形.
解:能出现平行四边形.根据题意得:AP=t,CQ=3t,
则PD=AD-AP=6-t,BQ=BC-CQ=16-3t,
∵E是BC的中点,
∴CE=8,
∵AD∥BC,
∴①当PD=CQ时,四边形CDPQ是平行四边形,
即6-t=3t,
解得:t=1.5;
∴当t=1.5时,四边形CDPQ是平行四边形;
 ②当Q运动到E和B之间,且PD=EQ时,四边形PDEQ是平行四边形,
②当Q运动到E和B之间,且PD=EQ时,四边形PDEQ是平行四边形,即3t-8=6-t,
解得:t=3.5,
∴当t=3.5时,四边形PDEQ是平行四边形;
③当Q运动到E和C之间,且PD=EQ时,四边形PDQE是平行四边形,
即8-3t=6-t,
解得:t=1,
∴当t=1时,四边形PDQE是平行四边形;
④当AP=BQ是,四边形ABQP是平行四边形,
即t=16-3t,
解得:t=4,
∴当t=4时,四边形ABQP是平行四边形.
点评:此题考查了梯形的性质、平行四边形的判定.此题难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列不等式中,总能成立的是( )
| A、a2>0 |
| B、2a>a |
| C、-a2≤0 |
| D、a2>a |
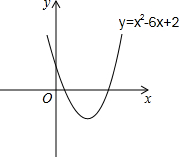 如图所示,已知抛物线y=x2-6x+2,将此抛物线沿x轴方向向左平移6个单位长度,得到一条新的抛物线.
如图所示,已知抛物线y=x2-6x+2,将此抛物线沿x轴方向向左平移6个单位长度,得到一条新的抛物线.