题目内容
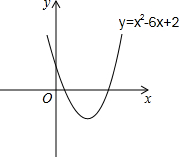 如图所示,已知抛物线y=x2-6x+2,将此抛物线沿x轴方向向左平移6个单位长度,得到一条新的抛物线.
如图所示,已知抛物线y=x2-6x+2,将此抛物线沿x轴方向向左平移6个单位长度,得到一条新的抛物线.(1)求平移后的抛物线的函数关系式.
(2)若直线y=m与这两条抛物线有且只有四个交点,求实数m的取值范围.
考点:抛物线与x轴的交点,二次函数图象与几何变换
专题:
分析:(1)先把原二次函数的解析式化为顶点式的形式,再根据二次函数平移的性质即可得出结论;
(2)求出两抛物线的交点及顶点坐标,进而可得出结论.
(2)求出两抛物线的交点及顶点坐标,进而可得出结论.
解答:解:(1)∵原函数可化为y=(x-3)2-7,
∴将此抛物线沿x轴方向向左平移6个单位长度后,抛物线的解析式为=(x+3)2-7;
(2)∵由(1)知,两抛物线的顶点坐标为(3,-7),(-3,-7),
则
,
解得
,
∴两抛物线的交点为(0,2),
∵直线y=m与这两条抛物线有且只有四个交点,
∴m>-7且m≠2.
∴将此抛物线沿x轴方向向左平移6个单位长度后,抛物线的解析式为=(x+3)2-7;
(2)∵由(1)知,两抛物线的顶点坐标为(3,-7),(-3,-7),
则
|
解得
|
∴两抛物线的交点为(0,2),
∵直线y=m与这两条抛物线有且只有四个交点,
∴m>-7且m≠2.
点评:本题考查的是抛物线与x轴的交点问题,熟知函数图象平移的性质是解答此题的关键.

练习册系列答案
相关题目
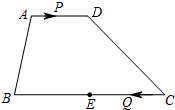 在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点,点P以每秒1个单位长度的速度从点A出发沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时点Q也随之停止运动.探究:在运动过程中,图中是否出现平行四边形?若能请写出平行四边形名称,并求出运动时间t;如不能,则说明理由.
在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点,点P以每秒1个单位长度的速度从点A出发沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时点Q也随之停止运动.探究:在运动过程中,图中是否出现平行四边形?若能请写出平行四边形名称,并求出运动时间t;如不能,则说明理由. 如图,在边长为1的正方形ABCD中,M是AD的中点,连接BM,BM的垂直平分线交BC的延长线于F,连接MF交CD于N.
如图,在边长为1的正方形ABCD中,M是AD的中点,连接BM,BM的垂直平分线交BC的延长线于F,连接MF交CD于N. 已知:如图,?ABCD中,AD=2AB,将CD向两边分别延长到E,F使CD=CE=DF.求证:AE⊥BF.
已知:如图,?ABCD中,AD=2AB,将CD向两边分别延长到E,F使CD=CE=DF.求证:AE⊥BF. 如图,正比例函数图象与一次函数y=-x+1的图象相交于点P,已知P点纵坐标为2.
如图,正比例函数图象与一次函数y=-x+1的图象相交于点P,已知P点纵坐标为2.