题目内容
因式分解:
①4x2-16
②m2(a-1)+9(1-a)
③x4-2x2+1.
①4x2-16
②m2(a-1)+9(1-a)
③x4-2x2+1.
考点:提公因式法与公式法的综合运用
专题:因式分解
分析:①先提取公因式4,再对余下的多项式利用平方差公式继续分解;
②先提取公因式(a-1),再对余下的多项式利用平方差公式继续分解;
③先利用完全平方公式分解因式,再利用平方差公式继续分解因式.
②先提取公因式(a-1),再对余下的多项式利用平方差公式继续分解;
③先利用完全平方公式分解因式,再利用平方差公式继续分解因式.
解答:解:①4x2-16
=4(x2-4)
=4(x+2)(x-2);
②m2(a-1)+9(1-a)
=(a-1)(m2-1)
=(a-1)(m+3)(m-3);
③x4-2x2+1
=(x2-1)2
=(x+1)2(x-1)2.
=4(x2-4)
=4(x+2)(x-2);
②m2(a-1)+9(1-a)
=(a-1)(m2-1)
=(a-1)(m+3)(m-3);
③x4-2x2+1
=(x2-1)2
=(x+1)2(x-1)2.
点评:本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
某次射击练习中,甲、乙两名同学的成绩(单位:环)如表,则这两名同学射击成绩的方差( )
| 选手 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
| 甲 | 5 | 6 | 8 | 7 | 9 |
| 乙 | 6 | 7 | 4 | 10 | 8 |
| A、甲的方差大 |
| B、乙的方差大 |
| C、甲、乙的方差一样大 |
| D、甲、乙的方差无法判断大小 |
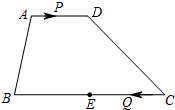 在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点,点P以每秒1个单位长度的速度从点A出发沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时点Q也随之停止运动.探究:在运动过程中,图中是否出现平行四边形?若能请写出平行四边形名称,并求出运动时间t;如不能,则说明理由.
在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点,点P以每秒1个单位长度的速度从点A出发沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时点Q也随之停止运动.探究:在运动过程中,图中是否出现平行四边形?若能请写出平行四边形名称,并求出运动时间t;如不能,则说明理由. 如图,在边长为1的正方形ABCD中,M是AD的中点,连接BM,BM的垂直平分线交BC的延长线于F,连接MF交CD于N.
如图,在边长为1的正方形ABCD中,M是AD的中点,连接BM,BM的垂直平分线交BC的延长线于F,连接MF交CD于N.