题目内容
某出版社出版适合中学生阅读的科普读物,该读物首次出版印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下表:
(1)通过对上表中数据的探究,你发现这种读物的投入成本y(元)是印数x(册)的正比例函数?还是一次函数?并求出这个函数的表达式(不要求写出x的取值范围);
(2)如果出版社投入成本60000元,那么能印该读物多少册?
| 印数x(册) | 5000 | 8000 | 11000 | 14000 | … |
| 成本y(元) | 28500 | 36000 | 43500 | 51000 | … |
(2)如果出版社投入成本60000元,那么能印该读物多少册?
考点:一次函数的应用
专题:销售问题
分析:(1)根据条件设投入成本y(元)是印数x(册)的一次函数解析式为y=kx+b,由待定系数法求出其解即可;
(2)将y=60000元代入(1)的解析式求出x的值即可.
(2)将y=60000元代入(1)的解析式求出x的值即可.
解答:解:(1)投入成本y(元)是印数x(册)的一次函数的解析式为y=kx+b,由题意,得
,
解得:
.
故所求的函数关系式为y=
x+16000;
(2)由题意,得
60000=
x+16000,
解得x=17600
答:能印该读物17600册.
|
解得:
|
故所求的函数关系式为y=
| 5 |
| 2 |
(2)由题意,得
60000=
| 5 |
| 2 |
解得x=17600
答:能印该读物17600册.
点评:本题考查了待定系数法求一次函数的解析式的运用,二元一次方程组的解法的运用,解答时运用待定系数法求出一次函数的解析式是关键.

练习册系列答案
相关题目
已知函数y=-
的图象上有两点P(x1,y1),Q(x2,y2),若x1<x2,则y1与y2的大小关系是( )
| 3 |
| x |
| A、y1=y2 |
| B、y1<y2 |
| C、y1<y2 |
| D、无法确定 |
已知点A(3,a+1)在x轴上,则a等于( )
| A、-1 | B、1 | C、0 | D、±1 |
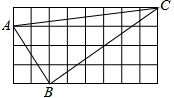 如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识回答问题.
如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识回答问题.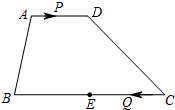 在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点,点P以每秒1个单位长度的速度从点A出发沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时点Q也随之停止运动.探究:在运动过程中,图中是否出现平行四边形?若能请写出平行四边形名称,并求出运动时间t;如不能,则说明理由.
在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点,点P以每秒1个单位长度的速度从点A出发沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时点Q也随之停止运动.探究:在运动过程中,图中是否出现平行四边形?若能请写出平行四边形名称,并求出运动时间t;如不能,则说明理由. 已知:如图,?ABCD中,AD=2AB,将CD向两边分别延长到E,F使CD=CE=DF.求证:AE⊥BF.
已知:如图,?ABCD中,AD=2AB,将CD向两边分别延长到E,F使CD=CE=DF.求证:AE⊥BF.