题目内容
2.已知在直角坐标系中,四边形ABCD四个顶点的坐标分别为A(-$\sqrt{3}$,-$\sqrt{2}$),B(1,-1),C($\sqrt{3}$,$\sqrt{2}$),D(-1,1).以点A,B,C,D为顶点的四边形是不是平行四边形?请给出证明.分析 由已知条件得出点A与点C关于原点对称,点B与点D关于原点对称,得出OA=OC,OB=OD,由平行四边形的判定方法即可得出结论.
解答 解:四边形是平行四边形;理由如下:
∵A(-$\sqrt{3}$,-$\sqrt{2}$),B(1,-1),C($\sqrt{3}$,$\sqrt{2}$),D(-1,1).
∴点A与点C关于原点对称,点B与点D关于原点对称,
∴OA=OC,OB=OD,
∴四边形是平行四边形.
点评 本题考查了平行四边形的判定方法、坐标与图形性质、关于原点对称的点的坐标特征;熟练掌握平行四边形的判定方法,由关于原点对称的点的坐标特征得出OA=OC,OB=OD是解决问题的关键.

练习册系列答案
相关题目
 如图,已知AB∥CD,CD⊥EF,垂足为N,AB与EF交于点M,求证:AB⊥EF.(用反证法证明)
如图,已知AB∥CD,CD⊥EF,垂足为N,AB与EF交于点M,求证:AB⊥EF.(用反证法证明) 如图,已知AB是⊙O的直径,AC是弦,BC=6cm,D为AC的中点,求OD的长.
如图,已知AB是⊙O的直径,AC是弦,BC=6cm,D为AC的中点,求OD的长.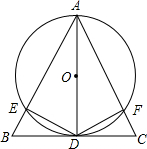 如图,在△ABC中,AB=AC,AD为△ABC的高,以AD为直径的⊙O与AB、AC两边分别交于点E、F,连接DE、DF.
如图,在△ABC中,AB=AC,AD为△ABC的高,以AD为直径的⊙O与AB、AC两边分别交于点E、F,连接DE、DF.