题目内容
11.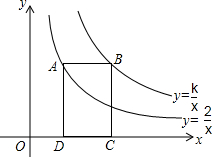 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,点C,D在x轴上.若四边形ABCD为矩形,且它的面积为3,则k=5.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,点C,D在x轴上.若四边形ABCD为矩形,且它的面积为3,则k=5.
分析 延长BA交y轴于E,如图,根据反比例函数k的几何意义得到S矩形BCOE=|k|,S矩形ADOE=|2|=2,则|k|-2=3,然后去绝对值即可得到满足条件的k的值.
解答  解:延长BA交y轴于E,如图,
解:延长BA交y轴于E,如图,
∵S矩形BCOE=|k|,S矩形ADOE=|2|=2,
而矩形ABCD的,面积为3,
∴S矩形BCOE-S矩形ADOE=3,
即|k|-2=3,
而k>0,
∴k=5.
故答案为5.
点评 本题考查了反比例函数系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
6.式子$\sqrt{2x-1}$在实数范围内有意义,则x的取值范围是( )
| A. | x<$\frac{1}{2}$ | B. | x≥0 | C. | x>$\frac{1}{2}$ | D. | x≥$\frac{1}{2}$ |
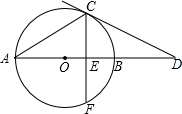 如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
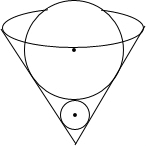 如图,在一个轴截面为等边三角形的圆锥形容器内放置两个密度相同的金属球,两球均与容器壁紧贴,且大球恰好压在小球上,则大球质量是小球的27倍.
如图,在一个轴截面为等边三角形的圆锥形容器内放置两个密度相同的金属球,两球均与容器壁紧贴,且大球恰好压在小球上,则大球质量是小球的27倍.