题目内容
15.解下列方程组:(1)$\left\{\begin{array}{l}{2x-3y=1}\\{2x-z=5}\\{x+3y+z=4}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+2y-z=2}\\{2x-3y+2z=2}\\{3x+4y+z=13}\end{array}\right.$.
分析 (1)②+③得3x+3y=9 ④,①+④得5x=10,解得x=2,将x=2代入①、②分别求得y、z;
(2)①×2+②得4x+y=6 ④,①+③得4x+6y=15 ⑤,⑤-④得5y=9,解得y=$\frac{9}{5}$,将y代入④求得x,将x、y代入①可得z.
解答 解:(1)$\left\{\begin{array}{l}{2x-3y=1}&{①}\\{2x-z=5}&{②}\\{x+3y+z=4}&{③}\end{array}\right.$,
②+③,得:3x+3y=9,④
①+④,得:5x=10,解得:x=2,
将x=2代入①得:4-3y=1,解得:y=1,
将x=2代入②得:4-z=5,解得:z=-1,
∴方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=-1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+2y-z=2}&{①}\\{2x-3y+2z=2}&{②}\\{3x+4y+z=13}&{③}\end{array}\right.$,
①×2+②得:4x+y=6,④
①+③得:4x+6y=15,⑤
⑤-④得:5y=9,解得:y=$\frac{9}{5}$,
将y=$\frac{9}{5}$代入④得:x=$\frac{21}{20}$,
将x=$\frac{21}{20}$、y=$\frac{9}{5}$代入①得:z=$\frac{53}{20}$,
∴方程组的解为$\left\{\begin{array}{l}{x=\frac{21}{20}}\\{y=\frac{9}{5}}\\{z=\frac{53}{20}}\end{array}\right.$.
点评 本题主要考查解三元一次方程组的能力,熟练掌握加减消元法是解题的关键.

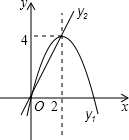 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1=y2,记M=y1=y2,下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有( )
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1=y2,记M=y1=y2,下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有( )| A. | ③④ | B. | ②③ | C. | ②④ | D. | ①④ |
| A. | 两组对边分别平行 | B. | 对角线相等 | ||
| C. | 对角线互相平行 | D. | 对角线互相垂直 |
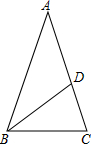 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )| A. | 30° | B. | 40° | C. | 36° | D. | 45° |
 如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )
如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )| A. | -10 | B. | 10 | C. | -8 | D. | 8 |
 在2016年宝应以“不忘初心,继续前进”为主题的青年千人毅行中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:
在2016年宝应以“不忘初心,继续前进”为主题的青年千人毅行中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据: