题目内容
18.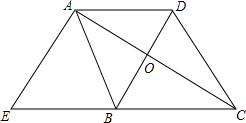 已知,如图,BD垂直平分AC,AE⊥AC,交CB的延长线于E,∠ABE=∠DCB.
已知,如图,BD垂直平分AC,AE⊥AC,交CB的延长线于E,∠ABE=∠DCB.(1)求证:四边形AEBD是平行四边形;
(2)若AE=EB=5,AB=6,求AC的长(BC≠6)
分析 (1)由BD垂直平分AC,得到AD=CD,AB=BC,AO=OC,根据平行线的判定和性质定理推出三角形全等的条件,由三角形全等得到AB=CD,AB=BC=CD=AD,得到四边形ABCD是菱形,得到∴AD∥BE,由AE⊥AC,得到AE∥BD,推出四边形AEBD是平行四边形;
(2)根据勾股定理即可求解.
解答 (!)证明:∵BD垂直平分AC,
∴AD=CD,AB=BC,AO=OC,
∵∠ABE=∠DCB,
∴AB∥CD,
∴∠BAC=∠DCO,∠ABO=∠CD0,
在△ABO与△CDO中,$\left\{\begin{array}{l}{∠BAC=∠DCO}\\{∠ABO=∠CDO}\\{AO=OC}\end{array}\right.$,
∴△ABO≌△CDO,
∴AB=CD
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,
∴AD∥BC,
∴AD∥BE,∵AE⊥AC,
∴AE∥BD,
∴四边形AEBD是平行四边形;
(2)解:由(1)知,四边形AEBD是平行四边形,
∴AD=BE,
∴CE=2BE=10,
∴AC=$\sqrt{{CE}^{2}{-AE}^{2}}$=5$\sqrt{3}$.
点评 本题考查了平行四边形的判定和性质,全等三角形的判定与性质,菱形的判定和性质,勾股定理的应用,掌握平行四边形的判定定理是解题的关键.

练习册系列答案
相关题目
8.下列一元二次方程中,没有实数根的是( )
| A. | x2-$\sqrt{2}$x=5 | B. | x(3x-5)-6=0 | C. | x2-x+1=0 | D. | x2-6x+9=0 |
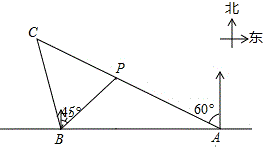 如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=8$\sqrt{6}$km,有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离(结果保留根号).
如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=8$\sqrt{6}$km,有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离(结果保留根号).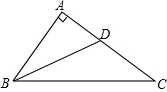 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AB=4,且点D到BC的距离为3,则BD=5.
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AB=4,且点D到BC的距离为3,则BD=5.