题目内容
3.某车间加工1300个零件后,采用了新工艺,工效提升了30%,这样加工同样多的零件就少用10h,采用新工艺前、后每时分别加工多少个零件?分析 设采用新工艺前每时加工x个零件,那么采用新工艺后每时加工1.3x个零件,根据时间=零件数÷每小时加工零件数,由等量关系:加工同样多的零件1300个少用10h,可列方程求解.
解答 解:设采用新工艺前每时加工x个零件,则采用新工艺后每时加工1.3x个零件,依题意有
$\frac{1300}{x}$-$\frac{1300}{1.3x}$=10,
解得x=30,
经检验:x=30是原分式方程的解,且符合题意,
则1.3x=39.
答:采用新工艺前每时加工30个零件,采用新工艺后每时加工39个零件.
点评 本题考查分式方程的应用和理解题意能力,关键是设出采用新工艺之前每小时加工x个,然后表示出采用新工艺后每小时加工多少个,再以时间做为等量关系列方程求解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
11.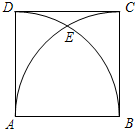 如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )
如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )
 如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )
如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )| A. | $\frac{2}{3}π$ | B. | π | C. | $\frac{4}{3}π$ | D. | $\frac{8}{3}π$ |
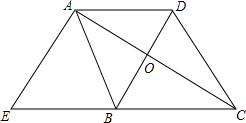 已知,如图,BD垂直平分AC,AE⊥AC,交CB的延长线于E,∠ABE=∠DCB.
已知,如图,BD垂直平分AC,AE⊥AC,交CB的延长线于E,∠ABE=∠DCB. 如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.
如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.