题目内容
8.下列一元二次方程中,没有实数根的是( )| A. | x2-$\sqrt{2}$x=5 | B. | x(3x-5)-6=0 | C. | x2-x+1=0 | D. | x2-6x+9=0 |
分析 分别计算出每个一元二次方程根的判别式即可判断.
解答 解:A、△=2-4(-5)=22>0,此方程有两不相等实数根;
B、原方程化简为3x2-5x-6=0,则有△=25-4×3(-6)=97>0,此方程有两不相等实数根;
C、△=1-4=-3<0,此方程没有实数根;
D、原方程配方得(x-3)2=0,此方程有两相等的根.
故选:C.
点评 本题考查了根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
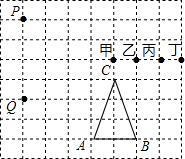 如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲、乙、丙、丁四点中的( )
如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲、乙、丙、丁四点中的( ) 如图所示,直线AB,CD相交于O,若∠1=40°,则∠2=140°.
如图所示,直线AB,CD相交于O,若∠1=40°,则∠2=140°.
 已知,如图,BD垂直平分AC,AE⊥AC,交CB的延长线于E,∠ABE=∠DCB.
已知,如图,BD垂直平分AC,AE⊥AC,交CB的延长线于E,∠ABE=∠DCB.