题目内容
给定一系列按规律排列的数:1,
,
,
,…,则这列数的第九个数是 .
| 4 |
| 3 |
| 3 |
| 2 |
| 8 |
| 5 |
考点:规律型:数字的变化类
专题:
分析:把1,
,
,
,…,变为
,
,
,
,…,可以看出分子是从2开始连续的偶数,分母是从2开始连续的自然数,由此得出第n个数为
,进一步得出答案即可.
| 4 |
| 3 |
| 3 |
| 2 |
| 8 |
| 5 |
| 2 |
| 2 |
| 4 |
| 3 |
| 6 |
| 4 |
| 8 |
| 5 |
| 2n |
| n+1 |
解答:解:∵1,
,
,
,…,
∴
,
,
,
,…,
∴第n个数为
,
则这列数的第九个数是
=
.
故答案为:
.
| 4 |
| 3 |
| 3 |
| 2 |
| 8 |
| 5 |
∴
| 2 |
| 2 |
| 4 |
| 3 |
| 6 |
| 4 |
| 8 |
| 5 |
∴第n个数为
| 2n |
| n+1 |
则这列数的第九个数是
| 2×9 |
| 9+1 |
| 9 |
| 5 |
故答案为:
| 9 |
| 5 |
点评:此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
下列各式运算中,正确的是( )
A、
| ||
| B、(-m3)4=m7 | ||
| C、-x12÷(-x)3=x9 | ||
| D、(a-b)2=a2-b2 |
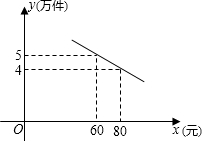 某商场销售一种市场需求较大的健身器材,已知每件产品的进价为40元,每年销售该种产品的总费用(不含进货费用)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元/件)之间存在着如图所示的一次函数关系.若商场希望该种产品一年的销售利润为40万元,请你为商场定一个销售单价.(年销售利润=年销售额-年销售产品进货总费用-年销售总费用)
某商场销售一种市场需求较大的健身器材,已知每件产品的进价为40元,每年销售该种产品的总费用(不含进货费用)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元/件)之间存在着如图所示的一次函数关系.若商场希望该种产品一年的销售利润为40万元,请你为商场定一个销售单价.(年销售利润=年销售额-年销售产品进货总费用-年销售总费用)