题目内容
11.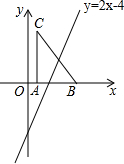 如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0),(8,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-4上时,线段BC扫过的面积为( )
如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0),(8,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-4上时,线段BC扫过的面积为( )| A. | 8$\sqrt{2}$ | B. | 16 | C. | 16$\sqrt{2}$ | D. | 32 |
分析 首先根据题意作出图形,则可得线段BC扫过的面积应为平行四边形BCC′B′的面积,其高是AC的长,底是点C平移的路程.则可由勾股定理求得AC的长,由点与一次函数的关系,求得A′的坐标,即可求得CC′的值,继而求得答案.
解答 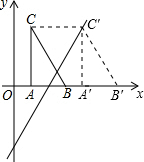 解:∵点A、B的坐标分别为(2,0)、(8,0),
解:∵点A、B的坐标分别为(2,0)、(8,0),
∴AB=6.
∵∠CAB=90°,BC=10,
∴AC=$\sqrt{1{0}^{2}-{6}^{2}}$=8.
∴A′C′=8.
∵点C′在直线y=2x-4上,
∴2x-4=8,解得:x=6.
即OA′=6.
∴CC′=AA′=OA′-OA=6-2=4,
∴S?BCC′B′=4×8=32,
即线段BC扫过的面积为32.
故选D.
点评 此题考查了一次函数的性质、平移的性质、勾股定理以及平行四边形的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
2.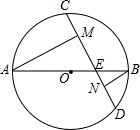 如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )
如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )
 如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )
如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | $\sqrt{2}$ |
19.为促进义务教育办学条件均衡,某市投入260万元资金为部分学校添置实验仪器,260万用科学记数法表示为( )
| A. | 260×103 | B. | 26×105 | C. | 2.6×105 | D. | 2.6×106 |
3.设x1、x2是一元二次方程x2+x-3=0的两根,则x13-4x22+15等于( )
| A. | -4 | B. | 8 | C. | 6 | D. | 0 |
 已知:如图,∠AOB=150°,OC平分∠AOB,∠AOD=90°,则∠COD的度数为15°.
已知:如图,∠AOB=150°,OC平分∠AOB,∠AOD=90°,则∠COD的度数为15°. 如图,在平行四边形ABCD中,AB=2,BC=4,AC的垂直平分线交AD于点E,则△CDE的周长为6.
如图,在平行四边形ABCD中,AB=2,BC=4,AC的垂直平分线交AD于点E,则△CDE的周长为6.