题目内容
20.已知关于x的方程x2+(2k+1)x+k2+2=0有两个实数根x1、x2.(1)求k的取值范围;
(2)若抛物线y=x2+(2k+1)x+k2+2与x轴交于A、B两点,O为坐标原点,且OA-OB=1,求k的值.
分析 (1)方程有两个实数根,则△≥0,代入系数即可求解;
(2)利用根与系数的关系将OA,OB的差用x1,x2的和差表示得到方程,从而得到答案.
解答 解:(1)∵方程x2+(2k+1)x+k2+2=0有两个实数根△≥0
(2k+1)2-4(k2+2)≥0
4k2+4k+1-4k2-14k-16≥0 解得:k≥$\frac{7}{4}$
(2)∵x1x2=k2+2≥0
∴A、B两点位于y轴的同侧
设A,B两点的坐标为(x1,0),(x2,0)
∵OB-OB=1,
∴AB=1,
∴|x1-x2|=1
(x1-x2)=1
(x1+x2)2-4x1x2=1
∴(2k+1)2-4(k2+2)=1
∴k=2
点评 本题将一元二次方程的根与系数关系和抛物线与x轴的交点整合,难点在于将点A与点B的距离用x1,x2的和差表示,有一定的难度.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
5.下列图案中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.化简$\frac{{a}^{2}}{a-1}$+$\frac{1}{1-a}$的结果是( )
| A. | a+1 | B. | $\frac{1}{a+1}$ | C. | a-1 | D. | $\frac{a}{a-1}$ |
10. 如图所示,是由相同的小正方体组成的几何体,其左视图是( )
如图所示,是由相同的小正方体组成的几何体,其左视图是( )
 如图所示,是由相同的小正方体组成的几何体,其左视图是( )
如图所示,是由相同的小正方体组成的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |




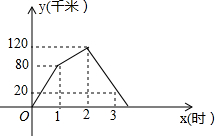 甲、乙两车均由A地向B地匀速行驶,甲车先出发,一段时间后乙车再出发,甲车到达B地后,立即按原路以另一速度匀速返回,直至两车相遇,设两车之间的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数关系图象如图所示.
甲、乙两车均由A地向B地匀速行驶,甲车先出发,一段时间后乙车再出发,甲车到达B地后,立即按原路以另一速度匀速返回,直至两车相遇,设两车之间的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数关系图象如图所示. 如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于点F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )
如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于点F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )


