题目内容
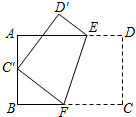如图，将矩形ABCD沿EF折叠，使顶点C落在AB边的中点c，上．若AB=6，BC=9，则BF的长为考点：翻折变换（折叠问题）
专题：
分析：如图，首先求出BC′的长度，设出C′F的长，根据勾股定理列出关于线段C′F的方程，解方程求出C′F的长，即可解决问题．
解答：解：∵四边形ABCD为矩形，
∴∠B=90°；
∵点C′为AB的中点，AB=6，
∴BC′=3；
由题意得：C′F=CF（设为x），
则BF=9-x；
由勾股定理得：
x2=32+（9-x）2，
解得：x=5，
∴BF=9-5=4．
故答案为4．
解：∵四边形ABCD为矩形，∴∠B=90°；
∵点C′为AB的中点，AB=6，
∴BC′=3；
由题意得：C′F=CF（设为x），
则BF=9-x；
由勾股定理得：
x2=32+（9-x）2，
解得：x=5，
∴BF=9-5=4．
故答案为4．
点评：该命题以矩形为载体，以翻折变换为方法，以考查翻折变换的性质、勾股定理的应用等几何知识点为核心构造而成；灵活运用有关定理来解题是关键．
练习册系列答案
相关题目
如图所示，阴影部分面积最大的是（ ）
A、 |
B、 |
C、 |
D、 |
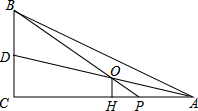如图，在△ABC中，∠C=90°，AC=8，AB=10，点P在AC上，AP=2，若AD平分∠BAC，且AD与BP相交于点O，OH⊥AC，计算线段OH的长度？
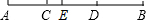如图，点C为线段AB上的一点，AC=
如图，已知AB⊥BD，AB∥ED，AB=ED，要说明△ABC≌△EDC，若以“SAS”为依据，还要添加的条件为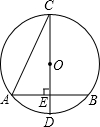
如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=2