题目内容
19.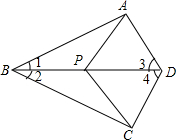 如图,在四边形ABCD中,点P是对角线BD上任意一点,∠1=∠2,∠3=∠4.求证:PA=PC.
如图,在四边形ABCD中,点P是对角线BD上任意一点,∠1=∠2,∠3=∠4.求证:PA=PC.
分析 先由ASA证明△ABD≌△CBD,得出AD=CD,再由SAS证明△APD≌△CPD,得出对应边相等即可.
解答 证明:在△ABD和△CBD中,
$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{BD=BD}&{\;}\\{∠3=∠4}&{\;}\end{array}\right.$,
∴△ABD≌△CBD(ASA),
∴AD=CD,
在△APD和△CPD中,
$\left\{\begin{array}{l}{AD=CD}&{\;}\\{∠3=∠4}&{\;}\\{PD=PD}&{\;}\end{array}\right.$,
∴△APD≌△CPD(SAS),
∴PA=PC.
点评 本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
2.下列各式的值相等的是( )
| A. | -32与-23 | B. | 32与|-2|3 | C. | -32与-(-3)2 | D. | (-3)2与-32 |
4.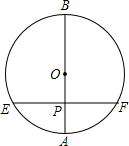 如图所示,在⊙O中,直径AB⊥弦EF,垂足为P,AP=1cm,BP=3cm,EF等于( )
如图所示,在⊙O中,直径AB⊥弦EF,垂足为P,AP=1cm,BP=3cm,EF等于( )
 如图所示,在⊙O中,直径AB⊥弦EF,垂足为P,AP=1cm,BP=3cm,EF等于( )
如图所示,在⊙O中,直径AB⊥弦EF,垂足为P,AP=1cm,BP=3cm,EF等于( )| A. | 2$\sqrt{3}$cm | B. | $\sqrt{3}$cm | C. | 2cm | D. | 4cm |
 如图所示,在△ABC中,AD是角平分线,DE∥AC交AB于E,EF∥AD交BC于F,试问:EF是△BDE的角平分线吗?说说你的理由.
如图所示,在△ABC中,AD是角平分线,DE∥AC交AB于E,EF∥AD交BC于F,试问:EF是△BDE的角平分线吗?说说你的理由.
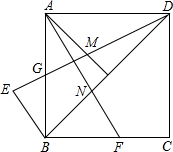 如图,在正方形ABCD中,G为AB边的中点,∠BAD的平分线交DG于M,过点B作BE⊥BD交DG的延长线于点E,再过点A作AF⊥DG,交BC边于点F,交BD边于点N.
如图,在正方形ABCD中,G为AB边的中点,∠BAD的平分线交DG于M,过点B作BE⊥BD交DG的延长线于点E,再过点A作AF⊥DG,交BC边于点F,交BD边于点N.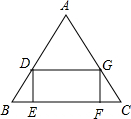 如图,在△ABC中BC=10,S△ABC=30,矩形DEFG内节接于△ABC,设DE的长为x,(1)写出矩形DEFG面积y与x的函数关系式及定义域;
如图,在△ABC中BC=10,S△ABC=30,矩形DEFG内节接于△ABC,设DE的长为x,(1)写出矩形DEFG面积y与x的函数关系式及定义域;