Question

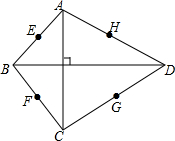在四边形ABCD中，AC⊥BD，边AB、BC、CD、DA的中点分别是E、F、G、H，求证：E、F、G、H四个点在同一的圆上．

Answer 1

考点：中点四边形

专题：证明题

分析：首先利用三角形的中位线定理证得四边形EFGH为平行四边形，然后利用有一个角是直角的平行四边形是矩形判定即可，则对角互补的四边形四点共圆．

解答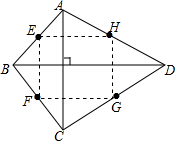：证明：如图，顺次连接点E、F、G、H．
∵点E、F、G、H分别是边AB、BC、CD、DA的中点，
∴EF=

1

2

AC，GH=

1

2

AC，
∴EF=GH，同理EH  FG
∴四边形EFGH是平行四边形；
又∵对角线AC、BD互相垂直，
∴EF与FG垂直．
∴四边形EFGH是矩形．
∴∠FEH=∠FGH=90°，
∴∠FEH+∠FGH=180°，
∴E、F、G、H四个点在同一的圆上．

点评：本题考查了中点四边形的知识，解题的关键是灵活运用三角形的中位线定理，平行四边形的判断及矩形的判断进行证明，是一道综合题．