题目内容
已知:AB=A′B′,AC=A′C′,AD为BC边的中线,A′D′为B′C′边的中线,AD=A′D′.求证:△ABC≌△A′B′C′.
考点:全等三角形的判定
专题:
分析:延长AD到点E使AD=DE,连接BE,延长A′D′到点E′使A′D′=D′E′,可证得△ADC≌△EDB,△A′D′C′≌△E′D′B′,进一步可证得△ABE≌△A′B′E′,可得出∠BAC=∠B′A′C′,可证明△ABC≌△A′B′C′.
解答: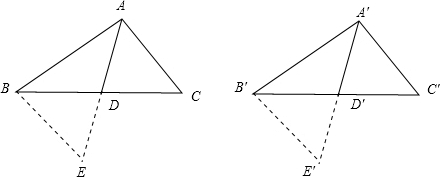 证明:如图,延长AD到点E使AD=DE,连接BE,延长A′D′到点E′使A′D′=D′E′,
证明:如图,延长AD到点E使AD=DE,连接BE,延长A′D′到点E′使A′D′=D′E′,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
∴BE=AC,
同理可理B′E′=A′C′,
∵AC=A′C′,
∴BE=B′E′,
∵AE=2AD,A′E′=2A′D′,且AD=A′D′,
∴AE=A′E′,
在△ABE和△A′B′E′中,
,
∴△ABE≌△A′B′E′(SSS),
∴∠BAE=∠B′A′E′,∠E=∠E′,
又∵∠E=∠DAC,∠E′=∠D′A′C′,
∴∠DAC=∠D′A′C′,
∴∠BAD+∠DAC=∠B′A′D′+∠D′A′C′,
即∠BAC=∠B′A′C′,
在△ABC和△A′B′C′中,
,
∴△ABC≌△A′B′C′(SAS).
 证明:如图,延长AD到点E使AD=DE,连接BE,延长A′D′到点E′使A′D′=D′E′,
证明:如图,延长AD到点E使AD=DE,连接BE,延长A′D′到点E′使A′D′=D′E′,在△ADC和△EDB中,
|
∴△ADC≌△EDB(SAS),
∴BE=AC,
同理可理B′E′=A′C′,
∵AC=A′C′,
∴BE=B′E′,
∵AE=2AD,A′E′=2A′D′,且AD=A′D′,
∴AE=A′E′,
在△ABE和△A′B′E′中,
|
∴△ABE≌△A′B′E′(SSS),
∴∠BAE=∠B′A′E′,∠E=∠E′,
又∵∠E=∠DAC,∠E′=∠D′A′C′,
∴∠DAC=∠D′A′C′,
∴∠BAD+∠DAC=∠B′A′D′+∠D′A′C′,
即∠BAC=∠B′A′C′,
在△ABC和△A′B′C′中,
|
∴△ABC≌△A′B′C′(SAS).
点评:本题主要考查全等三角形的判定和性质,证明出∠BAC=∠B′A′C′是解题的关键.

练习册系列答案
相关题目
关于x的一元二次方程x2+mx-1=0的根的情况为( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、不能确定 |
下列关于邻补角的说法,正确的是( )
| A、和为180°的两个角互为邻补角 |
| B、有公共顶点且互补的两个角互为邻补角 |
| C、有一条公共边且有一条公共边,另一边互为反向延长线的两个角互为邻补角 |
| D、有公共顶点且有一条公共边,另一边互为反向延长线的两个角互为邻补角 |
 如图所示,在O点的观测站测得渔船A、B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.
如图所示,在O点的观测站测得渔船A、B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.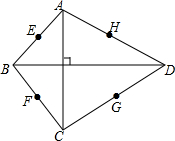 在四边形ABCD中,AC⊥BD,边AB、BC、CD、DA的中点分别是E、F、G、H,求证:E、F、G、H四个点在同一的圆上.
在四边形ABCD中,AC⊥BD,边AB、BC、CD、DA的中点分别是E、F、G、H,求证:E、F、G、H四个点在同一的圆上.