题目内容
17．
如图，在△ABC中，∠C=90°，AB=8，cosB=$\frac{3}{4}$，则BC的长是6．
分析 利用余弦函数的定义即可直接求解．
解答 解：∵在直角△ABC中，cosB=$\frac{BC}{AB}$=$\frac{BC}{8}$=$\frac{3}{4}$，
∴BC=6．
故答案是：6．
点评 本题考查了解直角三角形，理解余弦函数的定义是关键．
练习册系列答案
名题金卷系列答案
相关题目
19．
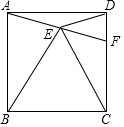如图，正方形ABCD中，以BC为边向正方形内部作等边△BCE，连接AE并延长交CD于F，连接DE，下列结论：①AE=DE；②∠CEF=45°；③AE=EF；④△DEF∽△ABE，其中正确的结论共有（ ）
如图，正方形ABCD中，以BC为边向正方形内部作等边△BCE，连接AE并延长交CD于F，连接DE，下列结论：①AE=DE；②∠CEF=45°；③AE=EF；④△DEF∽△ABE，其中正确的结论共有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
8．已知⊙O的半径为3cm，点P在⊙O内，则OP不可能等于（ ）
| A． | 1cm | B． | 1.5cm | C． | 2cm | D． | 3cm |
5．
已知如图，CO、CB是⊙O′的弦，⊙O′与坐标系x、y轴交于B、A两点，点A的坐标为（0，1），⊙O′的弦OB的长为$\sqrt{3}$，则∠OCB的度数为（ ）
已知如图，CO、CB是⊙O′的弦，⊙O′与坐标系x、y轴交于B、A两点，点A的坐标为（0，1），⊙O′的弦OB的长为$\sqrt{3}$，则∠OCB的度数为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
12．p+q=0，抛物线y=x2+px+q必经过（ ）
| A． | （-1，1） | B． | （1，-1） | C． | （-1，-1） | D． | （1，1） |
如图，在屋顶的斜坡面上安装太阳能热水器：先安装支架AB和CD（均与水平面垂直），再将集热板安装在AD上．为使集热板吸热率更高，公司规定：AD与水平面夹角为θ1，且在水平线上的投影AF为140 cm．现已测量出屋顶斜面与水平面夹角为θ2，并已知tanθ1=1.082，tanθ2=0.412．如果安装工人确定支架AB高为25 cm，求支架CD的高（结果精确到1 cm）．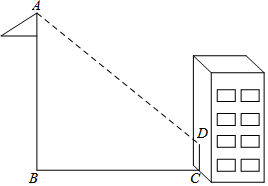
数学兴趣小组的同学们，想利用自己所学的数学知识测量学校旗杆的高度：下午活动时间，兴趣小组的同学们来到操场，发现旗杆的影子有一部分落在了墙上（如图所示）．同学们按照以下步骤进行测量：测得小明的身高1.65米，此时其影长为2.5米；在同一时刻测量旗杆影子落在地面上的影长BC为9米，留在墙上的影高CD为2米，请你帮助兴趣小组的同学们计算旗杆的高度．
如图，直线AB、CD相交于点E，DF∥AB，若∠D=70°，则∠CEB的度数为110°．