题目内容
11.已知抛物线y=x2-6x+8与x轴交于A、B两点,与y轴交于点C.(I)求△ABC的周长;
(2)求△ABC的面积.
分析 (1)先计算出自变量为0时的函数值得到C(0,8),再通过解方程x2-6x+8=0得到A、B点的坐标,接着利用勾股定理分别计算出AB、BC、AC,然后计算出△ABC的周长$\sqrt{5}$;
(2)利用三角形面积公式计算△ABC的面积.
解答 解:(1)当x=0时,y=x2-6x+8=8,则C(0,8);
当y=0时,x2-6x+8=0,解得x1=2,x2=4,则A、B点的坐标为(2,0),(4,0),
所以AB=2,AC=$\sqrt{{2}^{2}+{8}^{2}}$=2$\sqrt{17}$,BC=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
所以△ABC的周长=2+2$\sqrt{17}$+4$\sqrt{5}$;
(2)△ABC的面积=$\frac{1}{2}$×8×2=8.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.

练习册系列答案
相关题目
1. 如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
 如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
2.把汽油以均匀的速度注入容积为60L的桶里.注入的时间和注入的油量如下表:
(1)求q与t的函数解析式.并判断q是否是t的正比例函数;
(2)求变量t的取值范围;
(3)求t=1.5,4.5时,q的对应值.
| 注入的时间(min) | 1 | 2 | 3 | 4 | 5 | 6 |
| 注入油量q(L) | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 |
(2)求变量t的取值范围;
(3)求t=1.5,4.5时,q的对应值.
19.若二次函数y=x2+bx+c的图象与x轴交于两点,与y轴的正半轴交于一点,且对称轴为x=1,则下列说法正确的是( )
| A. | 二次函数的图象与x轴的交点位于y轴的两侧 | |
| B. | 二次函数的图象与x轴的交点位于y轴的右侧 | |
| C. | 其中二次函数中的c>1 | |
| D. | 二次函数的图象与x轴的一个交于位于x=2的右侧 |
6.小雷为表示出自己七年级几次数学测试成绩的变化情况,他应该采用的统计图是( )
| A. | 折线统计图 | B. | 条形统计图 | C. | 扇形统计图 | D. | 以上均可以 |
16.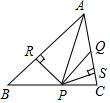 如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )
如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )
 如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )
如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )| A. | 全部正确 | B. | 仅①正确 | C. | 仅①、②正确 | D. | 仅①、③正确 |
20.已知三角形的两边长分别为4和6,则第三边的中线长x的取值范围是( )
| A. | 1<x<5 | B. | 2<x<10 | C. | 4<x<20 | D. | 无法确定 |
1.已知点在线段上,下列条件中不能确定点C是线段AB中点的是( )
| A. | AC=BC | B. | AB=2AC | C. | AC+BC=AB | D. | $BC=\frac{1}{2}AB$ |