题目内容
5.我校为更好地开展体育活动,就购买单价为30元的排球和单价为80元的篮球共100个.(1)设购买排球数为x(个),购买两种球的总费用为y(元),请你写出y与x的函数关系式(不要求写出自变量的取值范围);
(2)如果购买两种球的总费用不超过6500元,并且篮球数不少于排球数的2倍,那么有几种购买方案?
(3)从节约开支的角度来看,在(2)的购买方案中,你认为怎样购买最合算?
分析 (1)根据排球和篮球总共买了100个可得出购买篮球100-x个,再根据“购买费用=排球单价×购买数量+篮球单价×购买数量”,即可得出y关于x的函数关系式;
(2)由购买两种球的总费用不超过6500元,以及篮球数不少于排球数的2倍,即可得出关于x的一元一次不等式,解不等式即可得出x的取值范围,由此即可得出各购买方案;
(3)利用一次函数系数小于0,结合(2)中的x的取值范围即可解决最值问题.
解答 解:(1)设购买排球数为x(个),购买两种球的总费用为y(元),则购买篮球100-x个,
依题意得:y=30x+80(100-x)=-50x+8000(0≤x≤100).
(2)依题意得:$\left\{\begin{array}{l}{-50x+8000≤6500}\\{100-x≥2x}\end{array}\right.$,
解得:30≤x≤33$\frac{1}{3}$.
∴有四种购买方案:第一种:购买排球30个、篮球70个;第二种:购买排球31个、篮球69个;第三种:购买排球32个、篮球68个;第四种:购买排球33个、篮球67个.
(3)在y=-50x+8000中,k=-50<0,
∴y随x的增大而减小,
∴当x=33时,y最小,最小值为6350.
故在(2)的购买方案中,购买排球33个、篮球67个最合算,购买总费用为6350元.
点评 本题考查了一次函数的应用以及解一元一次方程组,解题的关键是:(1)利用数量关系找出函数关系式;(2)利用数量关系找出关于x的一元一次不等式;(3)利用一次函数的性质解决最值问题.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出不等式(不等式组或函数关系式)是关键.

练习册系列答案
相关题目
15.面积为2的正方形的边长在( )
| A. | 0和1之间 | B. | 1和2之间 | C. | 2和3之间 | D. | 3和4之间 |
20.我市气象部门测得某周内七天的日温差数据如下:4,6,6,5,7,6,8(单位:℃),这组数据的平均数和众数分别是( )
| A. | 7,6 | B. | 6,5 | C. | 5,6 | D. | 6,6 |
10.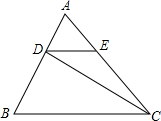 如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
 如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )| A. | 1:5 | B. | 1:12 | C. | 1:8 | D. | 1:9 |
17.下列备选答案的四个数中,最大的一个是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
 如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( ) 如图,点A、B、C、D在⊙O上,且四边形OABC为菱形,则∠ADC=60°.
如图,点A、B、C、D在⊙O上,且四边形OABC为菱形,则∠ADC=60°.