题目内容
20.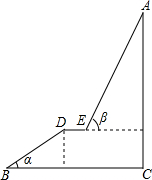 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为160米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25).
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为160米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25).
分析 在Rt△BFD中,根据正弦的定义求出DF的长,得到CG的长,进一步得到AG,再在Rt△AGE中,根据正弦的定义求出AE的长,即可得到答案.
解答  解:如图,作DF⊥BC,
解:如图,作DF⊥BC,
在Rt△BFD中,∵sin∠DBF=$\frac{DF}{BD}$,
∴DF=100×$\frac{1}{2}$=50米,
∴GC=DF=50米,
∴AG=AC-GC=200.4-50=150.4米,
在Rt△AGE中,∵sin∠AEG=$\frac{AG}{AE}$,
∴AE=$\frac{AG}{sin70°}$=$\frac{150.4}{0.94}$=160米.
故答案为:160.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念和坡角的概念是解题的关键,解答时注意:正确作出辅助线构造直角三角形准确运用锐角三角函数的概念列出算式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.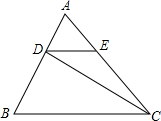 如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
 如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )| A. | 1:5 | B. | 1:12 | C. | 1:8 | D. | 1:9 |
12.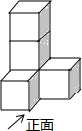 由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )
由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )
 由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )
由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )| A. | 左视图与俯视图相同 | B. | 左视图与主视图相同 | ||
| C. | 主视图与俯视图相同 | D. | 三种视图都相同 |
10.计算3x3•(-2x2)的结果是( )
| A. | -6x5 | B. | -6x6 | C. | -x5 | D. | x5 |
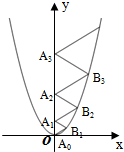 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2016在y轴的正半轴上,B1,B2,B3,…,B2016 在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2015B2016A2016都为等边三角形,则△A2015B2016A2016的边长=2016.
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2016在y轴的正半轴上,B1,B2,B3,…,B2016 在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2015B2016A2016都为等边三角形,则△A2015B2016A2016的边长=2016.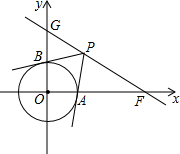 如图,在平面直角坐标系中,O为坐标原点,已知点F(2$\sqrt{3}$,0),直角GF交y轴正半轴于点G,且∠GFO=30°.
如图,在平面直角坐标系中,O为坐标原点,已知点F(2$\sqrt{3}$,0),直角GF交y轴正半轴于点G,且∠GFO=30°.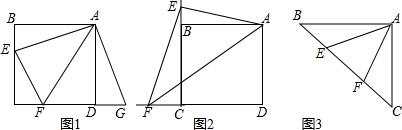
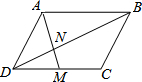 如图,在平行四边形ABCD中,如果点M为CD的中点,AM与BD相交于点N,若已知S△DMN=3,那么S△BAN等于( )
如图,在平行四边形ABCD中,如果点M为CD的中点,AM与BD相交于点N,若已知S△DMN=3,那么S△BAN等于( )