题目内容
14.分解因式:(1)6a2b-4a3b3-2ab
(2)25m2-n2
(3)4x2+12xy+9y2
(4)a2(x-y)-b2(x-y)
(5)-2a2x4+16a2x2-32a2
(6)(a2-a)2-(a-1)2.
分析 (1)直接提取公因式2ab即可;
(2)利用平方差公式分解因式;
(3)利用完全平方公式分解因式;
(4)先提取公因式(x-y),再对余下的多项式利用平方差公式继续分解;
(5)此多项式有公因式,应先提取公因式,再对余下的多项式进行观察,有3项,可采用完全平方公式和继续分解,再利用平方差公式分解因式;
(6)先利用利用平方差公式分解因式,再利用完全平方公式分解因式和平方差公式分解因式.
解答 解:(1)6a2b-4a3b3-2ab=2ab(3a-2a2b2-1);
(2)25m2-n2=(5m+n)(5m-n);
(3)4x2+12xy+9y2=(2x+3y)2;
(4)a2(x-y)-b2(x-y)
=(x-y)(a2-b2)
=(x-y)(a+b)(a-b);
(5)-2a2x4+16a2x2-32a2
=-2a2(x4+8x2-16)
=-2a2(x2-4)2
=-2a2(x+2)2(x-2))2;
(6)(a2-a)2-(a-1)2
=(a2-a+a-1)(a2-a-a+1)
=(a2-1)(a2-2a+1)
=(a+1)(a-1)(a-1)2
=(a+1)(a-1)3.
点评 本题考查了提公因式法与公式法分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
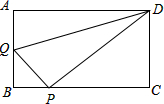 在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题: 如图,已知O是直线MN上的一点,∠AOB=90°,经过点O的直线DC平分∠BON,∠1=38°,求∠3和∠DOA的度数.
如图,已知O是直线MN上的一点,∠AOB=90°,经过点O的直线DC平分∠BON,∠1=38°,求∠3和∠DOA的度数.