题目内容
9.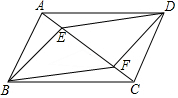 如图,在四边形ABCD中,AB∥CD,点E、F是对角线AC上两点,且∠ABF=∠CDE,AE=CF
如图,在四边形ABCD中,AB∥CD,点E、F是对角线AC上两点,且∠ABF=∠CDE,AE=CF(1)求证:△ABF≌△CDE;
(2)当四边形ABCD的边AB,AD满足什么条件时,四边形BFDE是菱形?说明理由.
分析 (1)由平行线的性质得出∠BAC=∠DCA.证出AF=CE.由AAS证明△ABF≌△CDE即可;
(2)先证明四边形ABCD是菱形,得出BD⊥AC,再证明四边形BFDE是平行四边形,即可得出结论.
解答 (1)证明:∵AB∥CD,
∴∠BAC=∠DCA.
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在△ABF和△CDE中,
$\left\{\begin{array}{l}{∠BAC=∠DCA}\\{∠ABF=∠CDE}\\{AF=CE}\end{array}\right.$,
∴△ABF≌△CDE(AAS);
(2)解:当四边形ABCD满足AB=AD时,四边形BEDF是菱形.理由如下: 连接BD交AC于点O,如图所示:
连接BD交AC于点O,如图所示:
由(1)得:△ABF≌△CDE,
∴AB=CD,BF=DE,∠AFB=∠CED,
∴BF∥DE.
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
又∵AB=AD,
∴平行四边形ABCD是菱形.
∴BD⊥AC.
∵BF=DE,BF∥DE,
∴四边形BEDF是平行四边形,
∴四边形BEDF是菱形.
点评 本题考查了平行线的性质、平行四边形的判定、菱形的判定与性质、全等三角形的判定与性质;熟练掌握菱形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
17.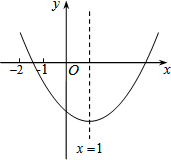 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①b2-4ac>0;②abc>0;③2a+b>0;④9a+3b+c<0;⑤8a+c>0.
其中,结论正确的个数是( )
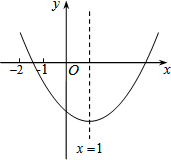 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③2a+b>0;④9a+3b+c<0;⑤8a+c>0.
其中,结论正确的个数是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
14.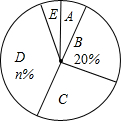 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
请你根据以上的信息,回答下列问题:
(1)被调查的学生中,最喜爱体育节目的有30人,这些学生数占被调查总人数的百分比为20%.
(2)被调查学生的总数为150人,统计表中m的值为45,统计图中n的值为36.
(3)在统计图中,E类所对应扇形圆心角的度数为21.6°.
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱新闻节目的学生数.
 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.| 类别 | A | B | C | D | E |
| 节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
| 人数 | 12 | 30 | m | 54 | 9 |
(1)被调查的学生中,最喜爱体育节目的有30人,这些学生数占被调查总人数的百分比为20%.
(2)被调查学生的总数为150人,统计表中m的值为45,统计图中n的值为36.
(3)在统计图中,E类所对应扇形圆心角的度数为21.6°.
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱新闻节目的学生数.
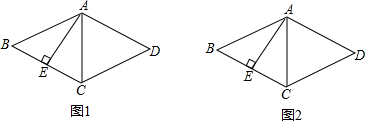
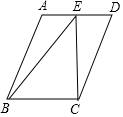 如图,面积为24的?ABCD中,BC=4,E是直线AD上一点,连接BE、CE,则sin∠BEC的最大值为$\frac{3}{5}$.
如图,面积为24的?ABCD中,BC=4,E是直线AD上一点,连接BE、CE,则sin∠BEC的最大值为$\frac{3}{5}$.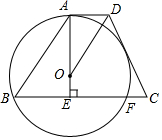 如图,梯形ABCD中,AD∥BC,AE⊥BC于E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
如图,梯形ABCD中,AD∥BC,AE⊥BC于E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.