题目内容
10. 如图,点A在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当AC=1时,△ABC的周长为$\sqrt{3}$+1.
如图,点A在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当AC=1时,△ABC的周长为$\sqrt{3}$+1.
分析 由OA的垂直平分线交OC于点B,可得出OB=AB,结合三角形的周长公式可得出△ABC的周长=OC+CA,由AC的长度利用反比例函数图象上点的坐标特征,即可得出点A的坐标,进而即可得出△ABC的周长.
解答 解:∵OA的垂直平分线交OC于点B,
∴OB=AB,
∴C△ABC=AB+BC+CA=OB+BC+CA=OC+CA.
∵点A在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,AC=1,
∴点A的坐标为($\sqrt{3}$,1),
∴C△ABC=OC+CA=$\sqrt{3}$+1.
故答案为:$\sqrt{3}$+1.
点评 本题考查了反比例函数图象上点的坐标特征以及线段垂直平分线的性质,根据线段垂直平分线的性质找出C△ABC=OC+CA是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
15. 如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
 如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )| A. | 传 | B. | 统 | C. | 文 | D. | 化 |
20.将一枚质地均匀的硬币先后抛掷两次,则至少出现一次正面向上的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
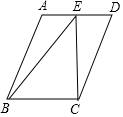 如图,面积为24的?ABCD中,BC=4,E是直线AD上一点,连接BE、CE,则sin∠BEC的最大值为$\frac{3}{5}$.
如图,面积为24的?ABCD中,BC=4,E是直线AD上一点,连接BE、CE,则sin∠BEC的最大值为$\frac{3}{5}$.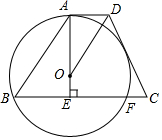 如图,梯形ABCD中,AD∥BC,AE⊥BC于E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
如图,梯形ABCD中,AD∥BC,AE⊥BC于E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.