题目内容
20.张老师给学生出了一道题:当x=2014,y=-2014时,求[(x2+y2)-(x-y)2+2y(x-1)]÷(4y)的值,题目出完后,小红说:“老师给的条件y=-2014是多余的”她的说法有道理吗?为什么?分析 先算乘法,再合并同类项,算除法,最后根据结果判断即可.
解答 解:小红的说法有道理.
理由:[(x2+y2)-(x-y)2+2y(x-1)]÷(4y)
=[x2+y2-x2+2xy-y2+2xy-2y]÷(4y)
=[4xy-2y]÷(4y)
=x-$\frac{1}{2}$.
原式的值域y的值没有关系,所以小红的说法有道理.
点评 本题考查了整式的混合运算和求值的应用,主要考查学生的计算能力和化简能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
1.下表为深圳市居民每月用水收费标准,(单位:元/m3).
(1)某用户用水10立方米,共交水费23元,求a的值;
(2)在(1)的前提下,该用户5月份交水费71元,请问该用户用水多少立方米?
| 用水量 | 单价 |
| x≤22 | a |
| 剩余部分 | a+1.1 |
(2)在(1)的前提下,该用户5月份交水费71元,请问该用户用水多少立方米?
11.已知x1,x2是一元二次方程x2+4x-3=0的两个实数根,则x1+x2-x1x2的值是( )
| A. | 6 | B. | 0 | C. | 7 | D. | -1 |
15. 如图,OC平分∠AOD,OD平分∠BOC,下列结论不成立的是( )
如图,OC平分∠AOD,OD平分∠BOC,下列结论不成立的是( )
 如图,OC平分∠AOD,OD平分∠BOC,下列结论不成立的是( )
如图,OC平分∠AOD,OD平分∠BOC,下列结论不成立的是( )| A. | ∠AOC=∠BOD | B. | ∠COD=$\frac{1}{2}$AOB | C. | ∠AOC=$\frac{1}{2}$∠AOD | D. | ∠BOC=2∠BOD |
12.下列不等式中,解集是x>1的不等式是( )
| A. | -3x>-3 | B. | -2x-3>-5 | C. | 2x+3>5 | D. | x+4>3 |
9.下列计算正确的是( )
| A. | a5+a5=a10 | B. | -a6•(-a)4=a10 | C. | (-bc)4÷(-bc)2=b2c2 | D. | (-ab)2•a=-a3b2 |
 如图,?ABCD的周长为60cm,△AOB的周长比△BOC大8cm,则 AB=19cm,BC=11cm.
如图,?ABCD的周长为60cm,△AOB的周长比△BOC大8cm,则 AB=19cm,BC=11cm.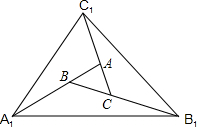 如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至A2,B2,C2,使得A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2…,按此规律继续下去.第n次操作得到△AnBnCn,则S1=7,△AnBnCn的面积Sn=7n.
如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至A2,B2,C2,使得A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2…,按此规律继续下去.第n次操作得到△AnBnCn,则S1=7,△AnBnCn的面积Sn=7n.