题目内容
18.黑板上写有1,$\frac{1}{2}$,$\frac{1}{3}$,…$\frac{1}{100}$共有100个数字,每次操作,先从黑板上的数选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+ab,则经过99次操作后,黑板上剩下的数是100.分析 经过99次操作后,黑板上剩下的数为x,则x+1=(1+1)×($\frac{1}{2}+1$)×($\frac{1}{3}$+1)×($\frac{1}{4}$+1)×…×($\frac{1}{99}$+1)×(1+$\frac{1}{100}$),整理可得x+1=101,解方程即可.
解答 解:∵a+b+ab+1=(a+1)(b+1),
∴每次操作前和操作后,黑板上的每个数加1后的乘积不变,
设经过99次操作后,黑板上剩下的数为x,则
x+1=(1+1)×($\frac{1}{2}+1$)×($\frac{1}{3}$+1)×($\frac{1}{4}$+1)×…×($\frac{1}{99}$+1)×(1+$\frac{1}{100}$),
化简得:x+1=101,
解得:x=100,
∴经过99次操作后,黑板上剩下的数是100.
故答案为:100.
点评 此题主要考查了推理与论证,关键是正确利用数据找出每次操作前和操作后黑板上剩下的数的规律.

练习册系列答案
相关题目
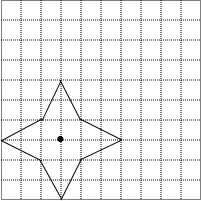 如图,一朵四瓣花飘动在10×10的网格中.
如图,一朵四瓣花飘动在10×10的网格中.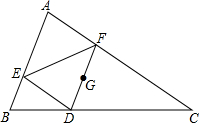 如图所示,在△ABC中,DF经过△ABC的重心G,且DF∥AB,DE∥AC,连接EF,如果BC=5,AC=$\sqrt{2}$AB,求证:△DEF∽△ABC.
如图所示,在△ABC中,DF经过△ABC的重心G,且DF∥AB,DE∥AC,连接EF,如果BC=5,AC=$\sqrt{2}$AB,求证:△DEF∽△ABC.
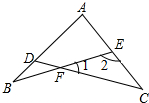 如图,∠B=25°,∠C=35°,∠A-∠1=60°,求∠A的度数.
如图,∠B=25°,∠C=35°,∠A-∠1=60°,求∠A的度数.