题目内容
4.对勾函数y=x+$\frac{1}{x}$具有以下性质:当x≥1时,y随x增大而增大,如:2≤x≤4,那么x=2,y有最小值2+$\frac{1}{2}$=$\frac{5}{2}$;当x=4时,y有最大值为4+$\frac{1}{4}$=$\frac{17}{4}$.请根据上述材料,完成一下问题:
(1)当3≤x≤5时,求函数y=x+$\frac{1}{x}$的最大值和最小值.
(2)0≤x≤2时,求函数y=x2+$\frac{1}{{x}^{2}+1}$-2的最大值和最小值.
分析 (1)根据已知条件,把x=3代入求得最小值,把x=5代入求得最大值即可;
(2)函数y=x2+$\frac{1}{{x}^{2}+1}$-2可以变形成y=x2+1+$\frac{1}{{x}^{2}+1}$-3,根据x的范围,求得x2+1的范围,即可求解.
解答 解:(1)当x=3时,y有最小值是3+$\frac{1}{3}$=$\frac{10}{3}$;
当x=5时,y有最大值是5+$\frac{1}{5}$=$\frac{26}{5}$;
(2)y=x2+$\frac{1}{{x}^{2}+1}$-2,即y=x2+1+$\frac{1}{{x}^{2}+1}$-3,
当0≤x≤2时x2+1的范围是:1≤x2+1≤5.
则当x2+1=1时,y有最小值是1+1-3=-1;
当x2+1=5时,y有最大值是5+$\frac{1}{5}$-3=$\frac{11}{5}$.
点评 本题考查了反比例函数的性质,正确理解y=x2+$\frac{1}{{x}^{2}+1}$-2与y=x+$\frac{1}{x}$之间形式上的关系是关键.

练习册系列答案
相关题目
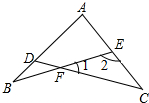 如图,∠B=25°,∠C=35°,∠A-∠1=60°,求∠A的度数.
如图,∠B=25°,∠C=35°,∠A-∠1=60°,求∠A的度数. 如图是2009年7月的台历,用“
如图是2009年7月的台历,用“ ”形框数,每次框出5个数.
”形框数,每次框出5个数.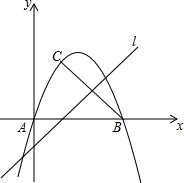 我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.已知二次函数y=kx2-(4k+1)x+3k+3.
我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.已知二次函数y=kx2-(4k+1)x+3k+3.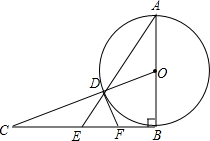 如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,点F为BE的中点.
如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,点F为BE的中点.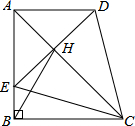 在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的个数是( )
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的个数是( )