题目内容
18. 如图,Rt△ABC中,∠C=90°,且AC=1,BC=2,则sin∠A=$\frac{2\sqrt{5}}{5}$.
如图,Rt△ABC中,∠C=90°,且AC=1,BC=2,则sin∠A=$\frac{2\sqrt{5}}{5}$.
分析 根据勾股定理先得出AB,再根据正弦的定义得出答案即可.
解答 解:∵∠C=90°,
∴AC2+BC2=AB2,
∵AC=1,BC=2,
∴AB=$\sqrt{5}$;
∴sin∠A=$\frac{BC}{AB}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
故答案为$\frac{2\sqrt{5}}{5}$.
点评 本题考查了锐角三角函数的定义,掌握正弦、余弦、正切的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列说法中,正确的是( )
| A. | 在数轴上表示-a的点一定在原点的左边 | |
| B. | 有理数a的倒数是$\frac{1}{a}$ | |
| C. | 一个数的相反数一定小于或等于这个数 | |
| D. | 如果|a|=-a,那么a是负数或零 |
 如图,海中有一个小岛B,它的周围14海里内有暗礁,在小岛正西方有一点A测得在北偏东60°,方向上有一灯塔C,灯塔C在小岛B北偏东15°方向上20海里处,渔船跟踪鱼群沿AC方向航行,每小时航行10$\sqrt{2}$海里.
如图,海中有一个小岛B,它的周围14海里内有暗礁,在小岛正西方有一点A测得在北偏东60°,方向上有一灯塔C,灯塔C在小岛B北偏东15°方向上20海里处,渔船跟踪鱼群沿AC方向航行,每小时航行10$\sqrt{2}$海里.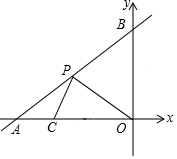 如图,直线y=x+6与x轴、y轴分别交于点A和点B,x轴上有一点C(-4,0),点P为直线一动点,当PC+PO值最小时点P的坐标为(-$\frac{9}{2}$,$\frac{3}{2}$).
如图,直线y=x+6与x轴、y轴分别交于点A和点B,x轴上有一点C(-4,0),点P为直线一动点,当PC+PO值最小时点P的坐标为(-$\frac{9}{2}$,$\frac{3}{2}$). 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若$\frac{AD}{AB}$=$\frac{4}{5}$,DE=8,则BC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若$\frac{AD}{AB}$=$\frac{4}{5}$,DE=8,则BC等于( )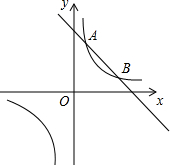 如图,一次函数y=k1+b与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于A(1,4),B(2,n)两点
如图,一次函数y=k1+b与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于A(1,4),B(2,n)两点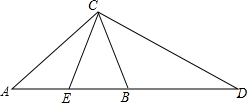 如图,已知△ABC中,AB=AC,CE是AB边上的中线,延长AB到点D,使BD=AB,求证:CD=2CE.
如图,已知△ABC中,AB=AC,CE是AB边上的中线,延长AB到点D,使BD=AB,求证:CD=2CE.