题目内容
19. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,求BE的长.
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,求BE的长.
分析 由线段垂直平分线的性质得出AE=BE,得出∠ABE=∠A,求出∠DBF,得出∠A=∠ABE=30°,由含30°角的直角三角形的性质即可得出结果.
解答 解:∵AB的垂直平分线DE交AC于E,交BC的延长线于F,
∴∠BDF=90°,AE=BE,
∴∠ABE=∠A,
∵∠F=30°,
∴∠DBF=60°,
∵∠ACB=90°,
∴∠A=30°,
∴∠ABE=30°,
∴BE=2DE=2.
点评 本题考查了含30°角的直角三角形的性质、线段垂直平分线的性质;根据题意求出∠ABE=30°是解决问题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
4.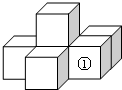 如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体从三个方向看的形状图,说法正确的是( )
如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体从三个方向看的形状图,说法正确的是( )
 如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体从三个方向看的形状图,说法正确的是( )
如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体从三个方向看的形状图,说法正确的是( )| A. | 从正面看改变,从左面看改变 | B. | 从上面看不变,从左面看不变 | ||
| C. | 从正面看不变,从上面看不变 | D. | 从上面看改变,从左面看不变 |
8.电影院第一排有m个座位,后面每一排比前一排多3个座位,则第n排的座位数有( )
| A. | m+3n | B. | mn+3 | C. | m+n+3 | D. | m+3n-3 |
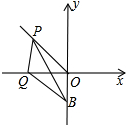 如图,已知B(0,-4)射线BO绕B点逆时针旋转30°,交第二象限角平分线于P点,线段PB绕P点顺时针旋转45°交x轴于Q点,求BQ长.
如图,已知B(0,-4)射线BO绕B点逆时针旋转30°,交第二象限角平分线于P点,线段PB绕P点顺时针旋转45°交x轴于Q点,求BQ长.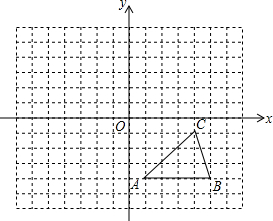 如图,在平面直角坐标系中,△ABC为格点三角形(顶点都是格点)且C(4,-1)
如图,在平面直角坐标系中,△ABC为格点三角形(顶点都是格点)且C(4,-1)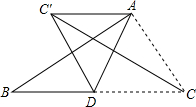 如图,AD是△ABC的边BC上的中线,且AD=BD=CD,把△ADC沿AD对折,点C落在点C′处,连接CC′,图中有哪些线段互相垂直?请一一写出来,并选择其中一组加以证明.
如图,AD是△ABC的边BC上的中线,且AD=BD=CD,把△ADC沿AD对折,点C落在点C′处,连接CC′,图中有哪些线段互相垂直?请一一写出来,并选择其中一组加以证明.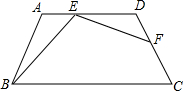 在梯形ABCD中,AD∥BC.AB=DC=AD=6,∠ABC=60°,点E、F分别在AD、DC上(点E与A、D不重合);且∠BEF=120°,设AE=x,DF=y.
在梯形ABCD中,AD∥BC.AB=DC=AD=6,∠ABC=60°,点E、F分别在AD、DC上(点E与A、D不重合);且∠BEF=120°,设AE=x,DF=y.