题目内容
12.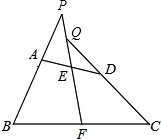 如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
分析 如图,连接BD,作BD的中点M,连接FM、EM.利用三角形中位线定理证得△EMF是等腰三角形,则∠MEF=∠MFE.利用三角形中位线定理、平行线的性质推知∠MEF=∠P,∠MFE=∠CQF.根据等量代换证得∠P=∠CQF.
解答 证明:如图,连接BD,作BD的中点M,连接EM、FM.
∵点E是AD的中点,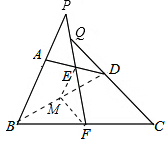
∴在△ABD中,EM∥AB,EM=$\frac{1}{2}$AB,
∴∠MEF=∠P
同理可证:FM∥CD,FM=$\frac{1}{2}$CD.
∴∠MFQ=∠CQF,
又∵AB=CD,
∴EM=FM,
∴∠MEF=∠MFE,
∴∠P=∠CQF..
点评 此题考查的是三角形中位线的性质、等腰三角形判定和性质等知识,解题的关键是题目中出现中点的条件想到添加三角形的中位线作为辅助线,属于中考常考题型.

练习册系列答案
相关题目
14.把分式$\frac{x-2y+z}{xyz}$中的x、y、z都扩大到原来的2倍,那么分式的值( )
| A. | 不变 | B. | 扩大到原来的2倍 | C. | 缩小到原来的$\frac{1}{2}$ | D. | 缩小到原来的$\frac{1}{4}$ |
11.已知二次函数y=x2的图象上有一点P(1,1),若将该抛物线平移后所得的二次函数表达式y=x2-2x-1,则点P经过该次平移后的坐标为( )
| A. | (2,1) | B. | (2,-1) | C. | (1,-2) | D. | (0,5) |
4.等式[(-6)-□]÷(-121)=0中,□表示的数是( )
| A. | 6 | B. | -6 | C. | 0 | D. | 115 |
 如图,已知∠EGB=90°,AD⊥BG,∠E=∠F.求证:AD是∠BAC平分线.
如图,已知∠EGB=90°,AD⊥BG,∠E=∠F.求证:AD是∠BAC平分线.