题目内容
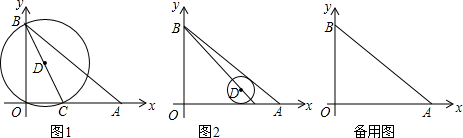
6.已知,平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6),C点坐标为(m,0)(0<m<8),D为线段BC上一点,以D为圆心,r为半径作⊙D.(1)如图1,若⊙D经过O、B两点,求证:点C在⊙D上;
(2)如图2,若⊙D与OA、AB相切,且m=6,求r;
(3)若r=1.5,且⊙D与△OAB的两边相切,求m的值.
分析 (1)连接OD,如图1,要证点C在⊙D上,只需证DC=DO,只需证∠COD=∠OCD,由∠BOC=90°及DO=DB,根据等角的余角相等即可解决问题;
(2)设⊙D与OA、AB分别相切于点E、点F,连接DE、DF、DA,如图2,根据切线的性质可得DE⊥OA,DF⊥AB.然后运用面积法(S△ABC=S△ADC+S△ADB),就可解决问题;
(3)可分三种情况讨论:①若⊙D与OA、OB分别相切于点E、H,连接DH、DE、OD,如图3①,运用面积法(S△ABC=S△ADC+S△ADB)就可求出m;②若⊙D与OA、AB分别相切于点E、F,连接DE、DF、AD,如图3②,运用面积法(S△ABC=S△ADC+S△ADB)就可求出m;③若⊙D与OB、AB分别相切于点H、F,点C作CN⊥AB于N,连接DH、DF,如图3③,根据切线的性质可得DH⊥OB,DF⊥AB,由DH=DF可得BC平分∠ABO,从而可证到Rt△BOC≌Rt△BNC,根据全等三角形的性质可得BN=BO=6,CN=OC=m,从而有AN=4,然后在Rt△CNA中运用勾股定理就可求出m.
解答 解:(1)连接OD,如图1,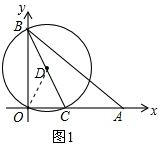
∵∠BOC=90°,
∴∠OBD+∠OCB=90°,∠BOD+∠COD=90°.
∵DO=DB,
∴∠OBD=∠BOD,
∴∠COD=∠OCD,
∴DC=DO,
∴点C在⊙D上;
(2)设⊙D与OA、AB分别相切于点E、点F,连接DE、DF、DA,如图2,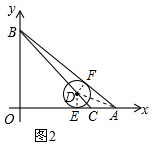
则有DE⊥OA,DF⊥AB.
∵A(8,0),B(0,6),C(6,0),
∴OA=8,OB=6,OC=6,
∴AB=10,AC=2.
∵S△ABC=S△ADC+S△ADB,
∴$\frac{1}{2}$×2×6=$\frac{1}{2}$×2r+$\frac{1}{2}$×10×r,
解得r=1;
(3)∵A(8,0),B(0,6),C(m,0),
∴OA=8,OB=6,OC=m,
∴AB=10,AC=8-m.
①若⊙D与OA、OB分别相切于点E、H,连接DH、DE、OD,如图3①,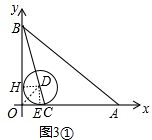
则有DE⊥OA,DH⊥OB.
∵S△BOC=S△ODC+S△ODB,
∴$\frac{1}{2}$×m×6=$\frac{1}{2}$×m×1.5+$\frac{1}{2}$×6×1.5,
解得m=2;
②若⊙D与OA、AB分别相切于点E、F,连接DE、DF、AD,如图3②,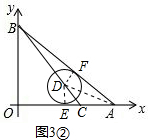
则有DE⊥OA,DF⊥AB.
∵S△ABC=S△ADC+S△ADB,
∴$\frac{1}{2}$×(8-m)×6=$\frac{1}{2}$×(8-m)×1.5+$\frac{1}{2}$×10×1.5,
解得m=$\frac{14}{3}$;
③若⊙D与OB、AB分别相切于点H、F,点C作CN⊥AB于N,连接DH、DF,如图3③,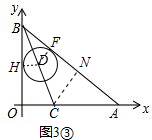
则有DH⊥OB,DF⊥AB,DH=DF,
∴BC平分∠ABO,即∠OBC=∠NBC.
在Rt△BOC和Rt△BNC中,
$\left\{\begin{array}{l}{∠OBC=∠NBC}\\{∠BOC=∠BNC=90°}\\{BC=BC}\end{array}\right.$,
∴Rt△BOC≌Rt△BNC,
∴BN=BO=6,CN=OC=m,
∴AN=10-6=4.
在Rt△CNA中,根据勾股定理可得
m2+42=(8-m)2,
解得m=3.
综上所述:m的值为2、3、$\frac{14}{3}$.
点评 本题主要考查了切线的性质、角平分线的判定与性质、等腰三角形的判定与性质、等角的余角相等、全等三角形的判定与性质、勾股定理等知识,有一定的综合性,运用分类讨论的思想是解决第(3)小题的关键,涉及到高(或垂线段)的长度时,常考虑使用面积法,应熟练掌握.

| A-C | C-D | E-D | E-F | G-F | B-G |
| 90m | 80m | 50 | -40m | -70m | 20m |
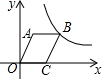 如图,在平行四边形OABC中,OC=3,OA=4,∠AOC=60°,若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,则k的值为10$\sqrt{3}$.
如图,在平行四边形OABC中,OC=3,OA=4,∠AOC=60°,若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,则k的值为10$\sqrt{3}$.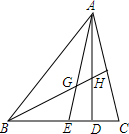 如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点G,AD与BF相交于点H,∠BAC=50°,∠C=70°,则∠AHB=120°.
如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点G,AD与BF相交于点H,∠BAC=50°,∠C=70°,则∠AHB=120°.