题目内容
6.将若干枚棋子平均分成三堆(每堆至少2枚),分别放在左边、中间、右边,并按如下顺序进行操作:第1次:从右边一堆中拿出2枚棋子放入中间一堆;
第2次:从左边一堆中拿出1枚棋子放入中间一堆;
第3次:从中间一堆中拿出几枚棋子放入右边一堆,并使右边一堆的棋子数为最初的2倍.
(1)操作结束后,若右边一堆比左边一堆多15枚棋子,问共有多少枚棋子?
(2)小明认为:无论最初的棋子数为多少,按上述方法完成操作后,中间一堆总是剩下1枚棋子,你同意他的看法吗?请说明理由.
分析 (1)根据题意,设最初每堆有x枚棋子,根据右边一堆比左边一堆多15枚棋子列方程求解即可.
(2)设原来平均每份a枚棋子,则最后右边2a枚棋子,左边(a-1)枚棋子,总棋子数还是3a,3a-2a-(a-1)=1,继而即可得出结论.
解答 解:(1)设最初每堆有x枚棋子,
依题意列等式:2x-(x-1)=15,
解得:x=14,
3x=42.
故共有42枚棋子;
(2)无论最初的棋子数为多少,最后中间只剩1枚棋子.
理由:设原来平均每堆a枚棋子,则最后左边2a枚棋子,右边(a-1)枚棋子,总枚棋子数还是3a.
3a-2a-(a-1)=1,
所以最后中间只剩1枚棋子.
点评 本题考查二元一次方程组的应用,解决问题的关键是读懂题意,找到所求的量的等量关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列多项式的乘法汇总,能用平方差公式计算的是( )
| A. | (3a+2b)(2a-3b) | B. | (3a-b)(-3a-b) | C. | (-a+b)(a-b) | D. | (x-2y)(-2y+x) |
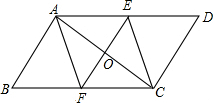 如图,已知在?ABCD中,点E、F分别在AD、BC上,O是AC的中点且EF⊥AC,求证:四边形AECF是菱形.
如图,已知在?ABCD中,点E、F分别在AD、BC上,O是AC的中点且EF⊥AC,求证:四边形AECF是菱形.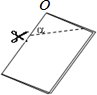 如图把一个矩形的纸片对折两次(折痕互相垂直且交点为O),然后剪下一个角,为了得到一个锐角为50° 的菱形,剪口与折痕所成角α的度数为25°或50°.
如图把一个矩形的纸片对折两次(折痕互相垂直且交点为O),然后剪下一个角,为了得到一个锐角为50° 的菱形,剪口与折痕所成角α的度数为25°或50°.