题目内容
回答下列问题:
(1)三条直线AB,CD,EF相交于一点O(如图1),图形中共有几对对顶角(平角除外)?几对邻补角?
(2)四条直线AB,CD,EF,GH相交于点O(如图2),图形中共有几对对顶角(平角除外)?几对邻补角?
(3)m条直线a1,a2,a3,…am-1,am相交于点O,则图中一共有几对对顶角(平角除外)?几对邻补角?
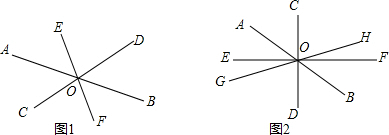
(1)三条直线AB,CD,EF相交于一点O(如图1),图形中共有几对对顶角(平角除外)?几对邻补角?
(2)四条直线AB,CD,EF,GH相交于点O(如图2),图形中共有几对对顶角(平角除外)?几对邻补角?
(3)m条直线a1,a2,a3,…am-1,am相交于点O,则图中一共有几对对顶角(平角除外)?几对邻补角?

考点:对顶角、邻补角
专题:规律型
分析:(1)根据对顶角、邻补角的定义得到3×2=6对对项角,12对邻补角;
(2)根据对顶角、邻补角的定义得到4×3=12对对项角,24对邻补角;
(3)根据前面的规律得到:有n条不同直线相交于一点,可以得到n(n-1)对对顶角,2n(n-1)对邻补角.
(2)根据对顶角、邻补角的定义得到4×3=12对对项角,24对邻补角;
(3)根据前面的规律得到:有n条不同直线相交于一点,可以得到n(n-1)对对顶角,2n(n-1)对邻补角.
解答:解:(1)有6对对顶角,12对邻补角;
(2)有12对对顶角,24对邻补角;
(3)由m条直线时,有m(m-1)对对顶角,2n(n-1)对邻补角;
(2)有12对对顶角,24对邻补角;
(3)由m条直线时,有m(m-1)对对顶角,2n(n-1)对邻补角;
点评:本题考查了对顶角、邻补角的定义;仔细观察图形弄清各个角之间的对顶角关系和邻补角关系是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
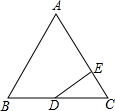 如图,△ABC是等边三角形,D为BC边的中点,DE⊥AC于点E.试探索线段CE与线段AC的数量关系,并说明理由.
如图,△ABC是等边三角形,D为BC边的中点,DE⊥AC于点E.试探索线段CE与线段AC的数量关系,并说明理由.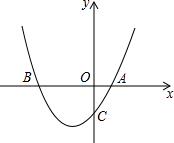 如图,已知二次函数y=ax2+bx+c经过点A(1,0),C(0,3),且对称轴为直线x=-1.
如图,已知二次函数y=ax2+bx+c经过点A(1,0),C(0,3),且对称轴为直线x=-1. 如图,试表示到点P的距离等于2.5cm的点的集合.
如图,试表示到点P的距离等于2.5cm的点的集合. 如图,直线AB,CD相交于点O,OE平分∠BOC,FO⊥CD于点O,若∠BOD:∠EOB=2:3,求∠AOF的度数.
如图,直线AB,CD相交于点O,OE平分∠BOC,FO⊥CD于点O,若∠BOD:∠EOB=2:3,求∠AOF的度数. 如图,已知∠AOC=108°,∠BOC=36°,试判断图中哪两个角互为补角,并说明理由.
如图,已知∠AOC=108°,∠BOC=36°,试判断图中哪两个角互为补角,并说明理由.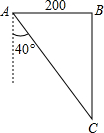 如图,东西两炮台A、B相距2000米,同时发现入侵舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离分别是多少米?(精确到1米)
如图,东西两炮台A、B相距2000米,同时发现入侵舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离分别是多少米?(精确到1米) 如图,四边形ABCD为⊙O的内接四边形,∠A=80°,若圆周长为18π,求
如图,四边形ABCD为⊙O的内接四边形,∠A=80°,若圆周长为18π,求