题目内容
19.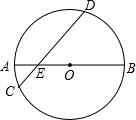 如图,在⊙O中.弦CD与直径AB相交于点E,且∠AEC=30°,AE=1cm,BE=5cm.求:
如图,在⊙O中.弦CD与直径AB相交于点E,且∠AEC=30°,AE=1cm,BE=5cm.求:(1)点O到CD的距离;
(2)弦CD的长.
分析 (1)因为∠AED=30°,可过点O作OF⊥CD于F,构成直角三角形,先求得⊙O的半径为3cm,进而求得OE=3-1=2,然后根据含30°角所对的直角边等于斜边的一半求得OF=1cm;
(2)根据勾股定理求得DF的长,然后由垂径定理求出CD的长.
解答 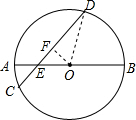 解:(1)过点O作OF⊥CD于F,连接DO,
解:(1)过点O作OF⊥CD于F,连接DO,
∵AE=1cm,BE=5cm,
∴AB=6cm,
∴⊙O的半径为3cm,
∴OE=3-1=2cm.
∵∠AEC=30°,
∴∠OEF=30°,
∴OF=$\frac{1}{2}$OE=1(cm);
故点O到CD的距离为1cm;
(2)∵OF=1cm,
∴DF=$\sqrt{O{D}^{2}-O{F}^{2}}$=2$\sqrt{2}$,
由垂径定理得:CD=2DF=4$\sqrt{2}$.
故CD的长为4$\sqrt{2}$cm.
点评 考查了勾股定理,垂径定理和含30度角的直角三角形.有关弦、半径、弦心距的问题常常利用它们构造的直角三角形来研究,所以连半径、作弦心距是圆中的一种常见辅助线添法.

练习册系列答案
相关题目