题目内容
9.已知a2-3a-1=0,求a2+$\frac{1}{{a}^{2}}$的值.分析 根据a2-3a-1=0,可得a≠0时,$a-3-\frac{1}{a}=0$,从而可得$a-\frac{1}{a}=3$,从而可以得到$(a-\frac{1}{a})^{2}=9$,然后展开化简即可解答本题.
解答 解:∵a2-3a-1=0,
∴当a≠0时,$a-3-\frac{1}{a}=0$,
∴$a-\frac{1}{a}=3$,
∴$(a-\frac{1}{a})^{2}=9$,
即${a}^{2}-2+\frac{1}{{a}^{2}}=9$,
故${a}^{2}+\frac{1}{{a}^{2}}=11$.
点评 本题考查探究性的问题,关键是可以根据题目中信息,进行正确的分析,推导出所要的结论.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 桌子上摆放着一个由若干个相同小正方体组成的几何体,其主视图和左视图如图所示,试画出它的俯视图.
桌子上摆放着一个由若干个相同小正方体组成的几何体,其主视图和左视图如图所示,试画出它的俯视图. 如图,正三角形ABC内接于圆O,设圆的半径为r,你能写出图中阴影部分的面积s与r之间的函数关系吗?你认为用哪种方法表示它们之间的函数关系比较方便?
如图,正三角形ABC内接于圆O,设圆的半径为r,你能写出图中阴影部分的面积s与r之间的函数关系吗?你认为用哪种方法表示它们之间的函数关系比较方便?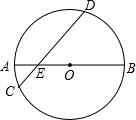 如图,在⊙O中.弦CD与直径AB相交于点E,且∠AEC=30°,AE=1cm,BE=5cm.求:
如图,在⊙O中.弦CD与直径AB相交于点E,且∠AEC=30°,AE=1cm,BE=5cm.求: