题目内容
3.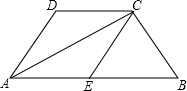 如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.
如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.
分析 首先根据平行四边形的判定方法,判断出四边形ADCE是平行四边形;然后判断出AE=CE,即可判断出四边形ADCE是菱形,据此解答即可.
解答 证明:∵AB∥DC,CE∥DA,
∴四边形ADCE是平行四边形,
∵AC平分∠BAD,
∴∠CAD=∠CAE,
又∵CE∥DA,
∴∠ACE=∠CAD,
∴∠ACE=∠CAE,
∴AE=CE,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形.
点评 此题主要考查了菱形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①菱形具有平行四边形的一切性质;②菱形的四条边都相等; ③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
13.计算(a-1)2,正确的结果是( )
| A. | a-2 | B. | a2 | C. | a-1 | D. | a |
14.过一条线段外一点,画出这条线段的垂线,垂足在( )
| A. | 这条线段上 | B. | 这条线段的端点 | ||
| C. | 这条线段的延长线上 | D. | 以上都有可能 |
 如图,点O为$\widehat{BC}$所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D=28°.
如图,点O为$\widehat{BC}$所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D=28°.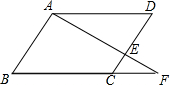 如图,?ABCD中,∠B=60°,过A作BA的垂线交CD于点E,交BC的延长线于点F,若S△CEF=9$\sqrt{3}$,求EF的长.
如图,?ABCD中,∠B=60°,过A作BA的垂线交CD于点E,交BC的延长线于点F,若S△CEF=9$\sqrt{3}$,求EF的长.