Question

10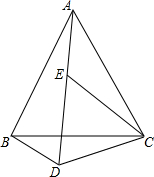．如图，已知点D是等边三角形ABC外的一点，将△BCD绕点C顺时针旋转至△ACE处．
（1）求旋转角的度数；
（2）求∠BDC的度数；
（3）证明：AD=BD+CD．

Answer 1

分析 （1）根据旋转角的定义，∠BCA计算旋转角，由此即可解决问题．
（2）先证明△DCE是等边三角形，推出∠DEC=60°，∠AEC=120°，再根据全等三角形性质∠BDC=∠AEC，由此即可解决问题．
（3）根据AD=AE+ED，只要证明AE=BD，DE=CD即可．

解答 解：（1）∵△ABC是等边三角形，
∴BC=AC，∠BCA=60°，
∵△ACE是由△BCD旋转得到，
∴∠BCA就是旋转角，
∴旋转角为60°．
（2）∵△ACE是由△BCD旋转得到，
∴∠DCE=∠BCA=60°，∠BDC=∠AEC，
∵CD=CE，
∴△CDE是等边三角形，
∴∠DEC=60°，
∠AEC=180°-∠DEC=120°，
∴∠BDC=120°．
（3）∵△BCD≌△ACE，△DEC是等边三角形，
∴AE=BD，DE=CD，
∵AD=AE+DE，
∴AD=BD+CD．

点评 本题考查三角形综合题、等边三角形的判定和性质、全等三角形的性质、旋转变换等知识，解题的关键是充分利用旋转不变性解决问题，发现△DEC是等边三角形是解题的突破口，属于中考常考题型．