题目内容
19.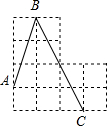 如图,每个小正方形的边长为1,点A、B、C是小正方形的顶点,则∠ABC的正弦值为( )
如图,每个小正方形的边长为1,点A、B、C是小正方形的顶点,则∠ABC的正弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 不能确定 |
分析 根据勾股定理即可得到AB,BC,AC的长度,可求∠ABC的度数,再根据正弦的定义求解即可.
解答  解:如图,连结AC,
解:如图,连结AC,
根据勾股定理可以得到:AC=BC=$\sqrt{10}$,AB=2$\sqrt{5}$.
∵($\sqrt{10}$)2+($\sqrt{10}$)2=(2$\sqrt{5}$)2.
∴AC2+BC2=AB2.
∴△ABC是等腰直角三角形.
∴∠ABC=45°,
∴∠ABC的正弦值为$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查了锐角三角函数的定义,勾股定理,判断△ABC是等腰直角三角形是解决本题的关键.

练习册系列答案
相关题目
10.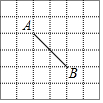 如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )
如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )
 如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )
如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )| A. | 7个 | B. | 8个 | C. | 10个 | D. | 12个 |
4.下列计算正确的是( )
| A. | 2x2+x3=2x5 | B. | (a-b)2=a2-b2 | C. | x5÷x=x5 | D. | x3•(2x)2=4x5 |
11.计算:-3+10=( )
| A. | -13 | B. | 7 | C. | -30 | D. | -7 |
 如图,将一副三角板的直角顶点O重叠在一起,若∠AOD=135度,则∠BOC=45度.
如图,将一副三角板的直角顶点O重叠在一起,若∠AOD=135度,则∠BOC=45度.