题目内容
10.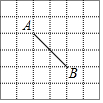 如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )
如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )| A. | 7个 | B. | 8个 | C. | 10个 | D. | 12个 |
分析 首先由勾股定理可求得AB的长,然后分别从BA=BC,AB=AC,CA=CB去分析求解即可求得答案.
解答 解:∵AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,如图所示:
∴①若BA=BC,则符合要求的有:C1,C2共2个点;
②若AB=AC,则符合要求的有:C3,C4共2个点;
③若CA=CB,则符合要求的有:C5,C6,C7,C8,C9,C10共6个点.
∴这样的C点有10个.
故选:C.
点评 本题考查了等腰三角形的判定以及勾股定理,解题关键是分类的数学思想.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
20.使式子$\frac{\sqrt{2-x}}{x}$有意义的实数x的取值范围是( )
| A. | x≤2 | B. | x<2且x≠0 | C. | x≤2且x≠0 | D. | x<2 |
2.“a是实数,|a|<0”这一事件是( )
| A. | 必然事件 | B. | 不确定事件 | C. | 不可能事件 | D. | 随机事件 |
19.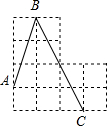 如图,每个小正方形的边长为1,点A、B、C是小正方形的顶点,则∠ABC的正弦值为( )
如图,每个小正方形的边长为1,点A、B、C是小正方形的顶点,则∠ABC的正弦值为( )
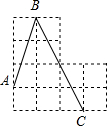 如图,每个小正方形的边长为1,点A、B、C是小正方形的顶点,则∠ABC的正弦值为( )
如图,每个小正方形的边长为1,点A、B、C是小正方形的顶点,则∠ABC的正弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 不能确定 |
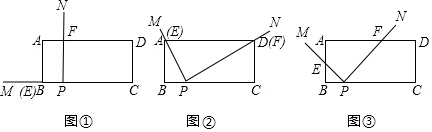
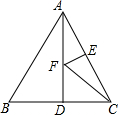 如图,等边△ABC中,AB=4,AD⊥BC于点D,点F在线段AD上运动,点E在AC上,且AE=2,当EF+CF取最小值时,∠ECF=30°.
如图,等边△ABC中,AB=4,AD⊥BC于点D,点F在线段AD上运动,点E在AC上,且AE=2,当EF+CF取最小值时,∠ECF=30°.