题目内容
4.下列计算正确的是( )| A. | 2x2+x3=2x5 | B. | (a-b)2=a2-b2 | C. | x5÷x=x5 | D. | x3•(2x)2=4x5 |
分析 根据整式运算的法则即可求出答案.
解答 解:(A)2x2与x3不是同类项,不能合并同类项,故A错误;
(B)(a-b)2=a2-2ab+b2,故B错误;
(C)x5÷x=x4,故C错误;
故选(D)
点评 本题考查整式的运算,涉及合并同类项项,完全平方公式,整式乘除法,属于基础题型.

练习册系列答案
相关题目
12.在《九章算术》中记载一道这样的题:“今有甲、乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,甲、乙持钱各几何?”题目大意是:甲、乙两人各带若干钱,如果甲得到乙所有钱的一半,那么甲共有钱50,如果乙得到甲所有钱的$\frac{2}{3}$,那么乙也共有钱50.甲、乙两人各需带多少钱?设甲需带钱x,乙带钱y,根据题意可列方程组为( )
| A. | $\left\{\begin{array}{l}{x+y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+2y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{1}{2}x+y=50}\\{x+\frac{2}{3}y=50}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+\frac{1}{2}y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ |
19.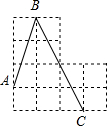 如图,每个小正方形的边长为1,点A、B、C是小正方形的顶点,则∠ABC的正弦值为( )
如图,每个小正方形的边长为1,点A、B、C是小正方形的顶点,则∠ABC的正弦值为( )
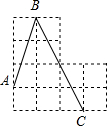 如图,每个小正方形的边长为1,点A、B、C是小正方形的顶点,则∠ABC的正弦值为( )
如图,每个小正方形的边长为1,点A、B、C是小正方形的顶点,则∠ABC的正弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 不能确定 |
16.若∠A为锐角,cosA=$\frac{\sqrt{2}}{2}$,则∠A的度数为( )
| A. | 75° | B. | 60° | C. | 45° | D. | 30° |
13.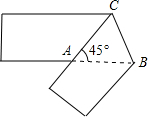 如图,将宽为1cm的长方形纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为( )
如图,将宽为1cm的长方形纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为( )
 如图,将宽为1cm的长方形纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为( )
如图,将宽为1cm的长方形纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为( )| A. | $\frac{\sqrt{3}}{2}$ cm2 | B. | $\sqrt{3}$ cm2 | C. | $\sqrt{2}$ cm2 | D. | $\frac{\sqrt{2}}{2}$ cm2 |
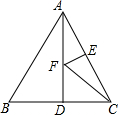 如图,等边△ABC中,AB=4,AD⊥BC于点D,点F在线段AD上运动,点E在AC上,且AE=2,当EF+CF取最小值时,∠ECF=30°.
如图,等边△ABC中,AB=4,AD⊥BC于点D,点F在线段AD上运动,点E在AC上,且AE=2,当EF+CF取最小值时,∠ECF=30°.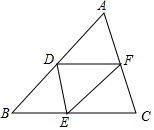 如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?