题目内容
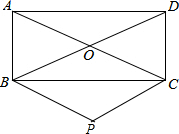如图，在矩形ABCD中，对角线AC与DB相交于点O，过点C作CP∥DB，过点B作BP∥AC，两线相交于点P．求证：四边形COBP是菱形．考点：菱形的判定
专题：证明题
分析：根据DP∥AC，CP∥BD，即可证出四边形ODPC是平行四边形，又知四边形ODPC是平行四边形，故可得OD=
BD=
AC=OC，即可证出四边形ODPC是菱形．
| 1 |
| 2 |
| 1 |
| 2 |
解答：证明：∵DP∥AC，CP∥BD
∴四边形ODPC是平行四边形，
∴OD=
BD=
AC=OC，
∴四边形ODPC是菱形．
∴四边形ODPC是平行四边形，
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形ODPC是菱形．
点评：本题主要考查矩形性质和菱形的判定的知识点，解答本题的关键是熟练掌握菱形的判定定理，此题比较简单．
练习册系列答案
相关题目
如果（m+3）x2-x+1=0是一元二次方程，则（ ）
| A、m≠-3 | B、m≠3 |
| C、m≠0 | D、m≠-3且m≠0 |
若关于x的一元二次方程的两个根为x1=2-
，x2=2+
，则这个方程是（ ）
| 3 |
| 3 |
| A、x2+4x+1=0 |
| B、x2-4x+1=0 |
| C、x2-4x-1=0 |
| D、x2+4x-1=0 |
如图，点A、B、C在☉O上，∠BAC=35°，那么∠BOC的度数是（ ）| A、35° | B、70° |
| C、30° | D、无法确定 |
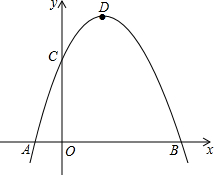如图，抛物线y=-x2+2x+3与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．